Ange funktionerna f och g sådan att....
Jag ska lösa följande uppgift....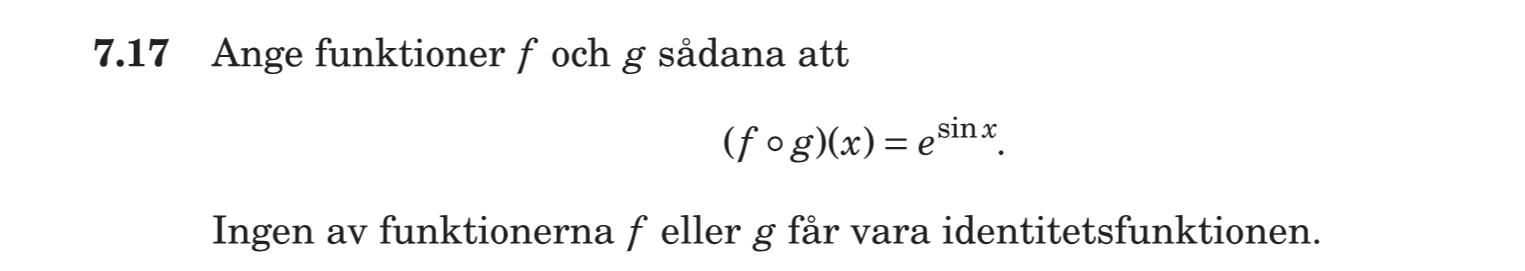
Jag vet att när dom säger (f o g)(x) betyder det att man kan skriva det som f(g(x)) = Men jag förstår inte hur jag kan komma vidare.
Ibland skrivs ex som exp(x)
Hur skulle du derivera esin(x)?
Jag hade derivat genom att tänka på följande: inre funktionen och yttre funktionen. e^x går ej att derivera så den stannar kvar vilket ger e^sin(x), medan derivatan för sin(x) blir till cos(x). så det ger e^sin(x) *cos(x)
Aha, så du gjorde en uppdelning i inre och yttre funktion intuitivt, och delade därmed upp funktionen i två funktioner: e^x och sin(x).
Jämför detta med vad du skulle göra i uppgiften.
Visa spoiler
Skriv ditt dolda innehåll här
Bazinga skrev:
Jag hade derivat genom att tänka på följande: inre funktionen och yttre funktionen. e^x går ej att derivera så den stannar kvar vilket ger e^sin(x), medan derivatan för sin(x) blir till cos(x). så det ger e^sin(x) *cos(x)
Hmmm, ”e^x går ej att derivera”, jag förstår hur du menar, men visst går det. Fast derivatan är också e^x.
Och skriv helst inte ”två funktioner: e^x och sin(x)”. Skriv hellre e^y och sin(x).
y och x är inte samma eftersom y = sin (x).
Lite märkligt... Förstår fortfarande inte varför det ändrar till e^y ?
Nvm jag löste.



