Andragradsekvationer ekvationssystem ma4

Förstår inte riktigt hur jag ska fortsätta
Visa att om 𝑧1 = 𝑎 + 𝑏𝑖 och 𝑧2 = 𝑎 − 𝑏𝑖 (a och b reella) är rötter till ekvationen
så är p och q reella.
Du har gjort ett misstag i första raden. Det stämmer inte att
z1z2 + pz1 + q = 0
Kommer du ihåg sambandet mellan p, q, och rötterna?
nej, skulle du kunna förklara?
1) Förstår du varför din första rad (z1z2 + pz1 + q = 0) inte stämmer?
2) Tyvärr vet jag inte om det diskuteras i klassen, men det finns ett väldigt intressant samband mellan rötterna, p och q:
z1 + z2 = -p
z1*z2 = q
1) jag gissar på att pz snarare ska behandlas som en konstant och en z term.
Nej.
I ekvationen z2 + pz + q = 0 ska z vara ett och samma tal. Antingen z1 (den första lösningen) eller z2 (den andra lösningen). Men du får inte kombinera z1 och z2.
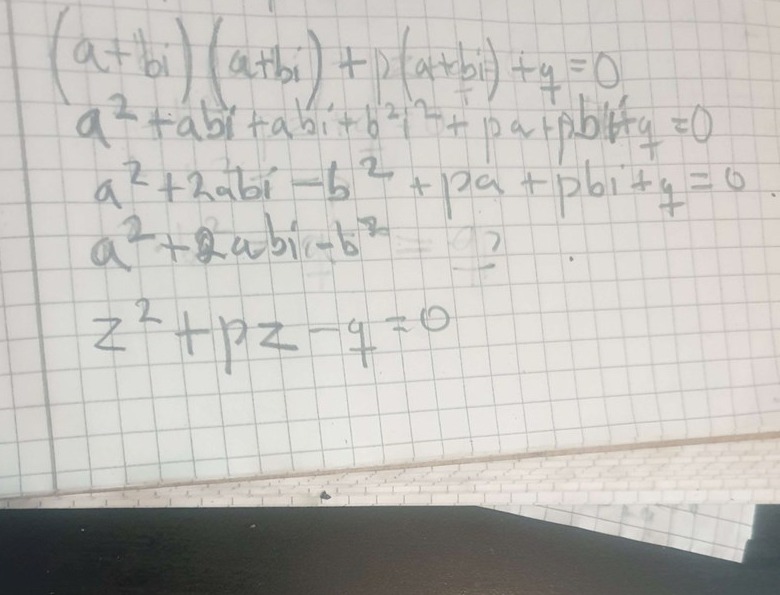
Hur ska jag tillämpa sambanden
För p:
p = -z1 - z2 = -(a+bi)-(a-bi) = -2a (som är ett reellt tal eftersom a är reellt)
Kan du göra det för q?

Jag har en fråga över det du gjorde. Skulle man kunna addera talen direkt eller blir det inte lika snyggt då?
Jag tycker att det är lika tydligt.
Okej, tack för hjälpen

