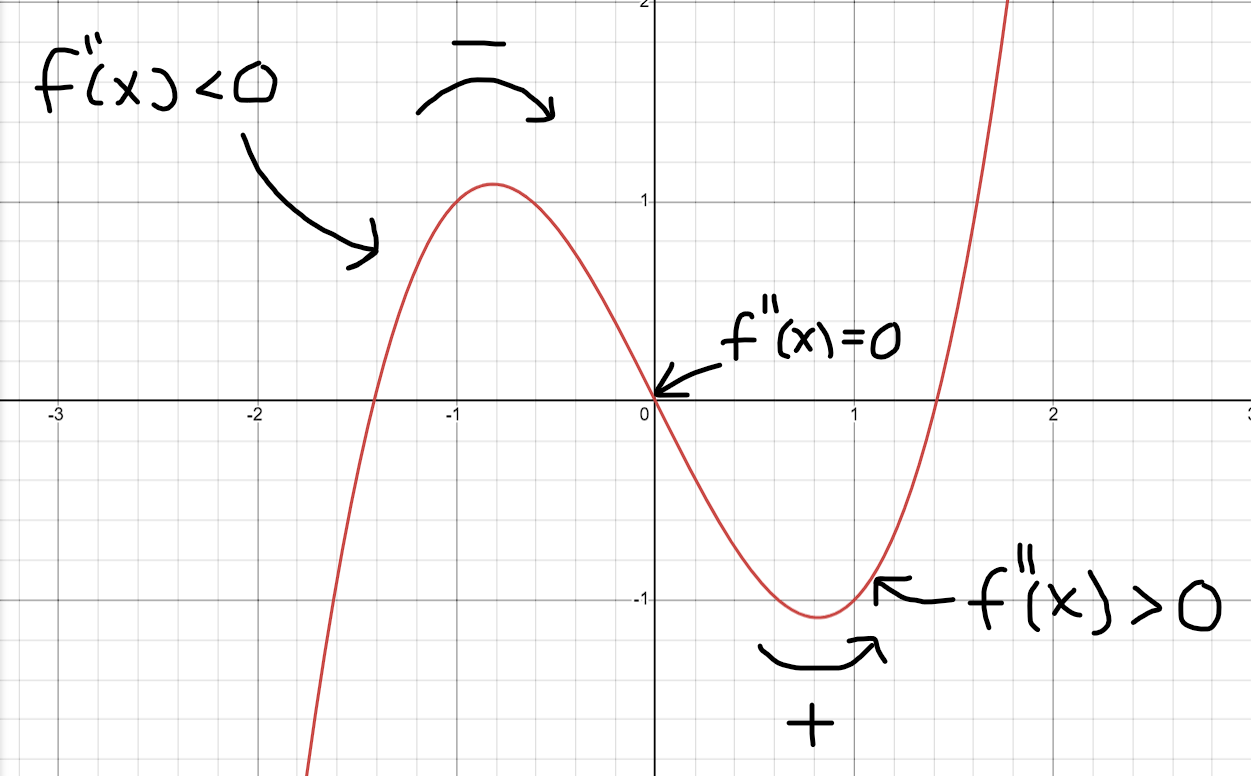
Andraderviatan av en graf
Hej,
jag förstår inte hur jag ska tänka med andraderivator och hur man läser av det från en graf.
Jag har kört fast med b-uppgiften på den här frågan men löst a-uppgiften.

Tacksam för svar på hur man ska tänka!
Första derivatan beskriver lutningen av en funktion, andraderivatan beskriver hur lutningen förändras, dvs om lutningen i sig ökar, minskar eller är konstant vid en viss punkt. Om f''(x)>0 så betyder det att lutningen ökar (konvex), om f''(x)<0 så minskar lutningen (konkav) och om f''(x)=0 har vi en inflektionspunkt, dvs där lutningen övergår från växande till avtagande eller tvärtom.
MathematicsDEF skrev:Första derivatan beskriver lutningen av en funktion, andraderivatan beskriver hur lutningen förändras, dvs om lutningen i sig ökar, minskar eller är konstant vid en viss punkt. Om f''(x)>0 så betyder det att lutningen ökar (konvex), om f''(x)<0 så minskar lutningen (konkav) och om f''(x)=0 har vi en inflektionspunkt, dvs där lutningen övergår från växande till avtagande eller tvärtom.
Tack så mycket, jag tror att jag förstår bättre nu, så en negativ andraderivata betyder att jag ska avläsa att lutningen inte är lika stark som den var till vänster om punkten?
Precis, det bästa sättet för mig personligen att komma ihåg vare sig andraderivatan är positiv eller negativ är genom att tänka avtagande eller växande lutning, exempelvis vid alla punkter till vänster om origo (x=0) så minskar lutningen "med tiden" eller längs x-axeln, vid x=0 så byter denna utveckling tecken och sedan till höger om origo så börjar lutningen istället att växa längs x-axeln.
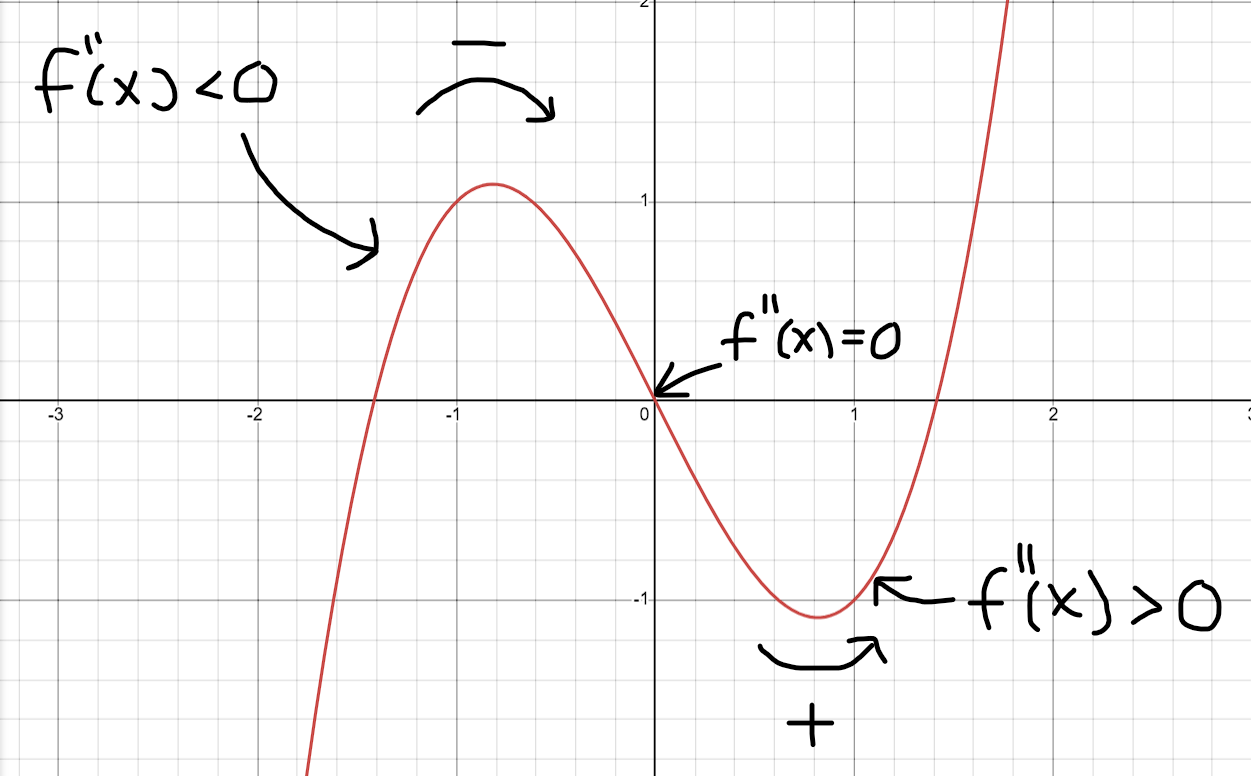
MathematicsDEF skrev:Precis, det bästa sättet för mig personligen att komma ihåg vare sig andraderivatan är positiv eller negativ är genom att tänka avtagande eller växande lutning, exempelvis vid alla punkter till vänster om origo (x=0) så minskar lutningen "med tiden" eller längs x-axeln, vid x=0 så byter denna utveckling tecken och sedan till höger om origo så börjar lutningen istället att växa längs x-axeln.
Okej, men mellan x=-0,8 och x=0 är inte andraderivatan positiv där eftersom lutningen hela tiden ökar när man rör sig åt höger?
Samma sak för x=0 och x=0,8, är inte andraderivatan mellan dom negativ?
Andraderivatan är negativ mellan -0.8 och 0 då lutningen hela tiden minskar tills x=0, då vänder det och lutningen börjar istället öka, det spelar ingen roll hur mycket eller lite det ökar utan man tittar bara på punkterna bredvid och avgör om lutningen är växande eller avtagande. Exempelvis vid ungefär x = -1 så är första derivatan positiv, men andraderivatan är ändå negativ då lutningen minskar om går till höger. Tänk dig att gå uppför en ramp eller backe som blir brantare och brantare , det representerar en positiv andraderivata, medan en skidbacke som blir brandare och brantare neråt är negativ andraderivata.
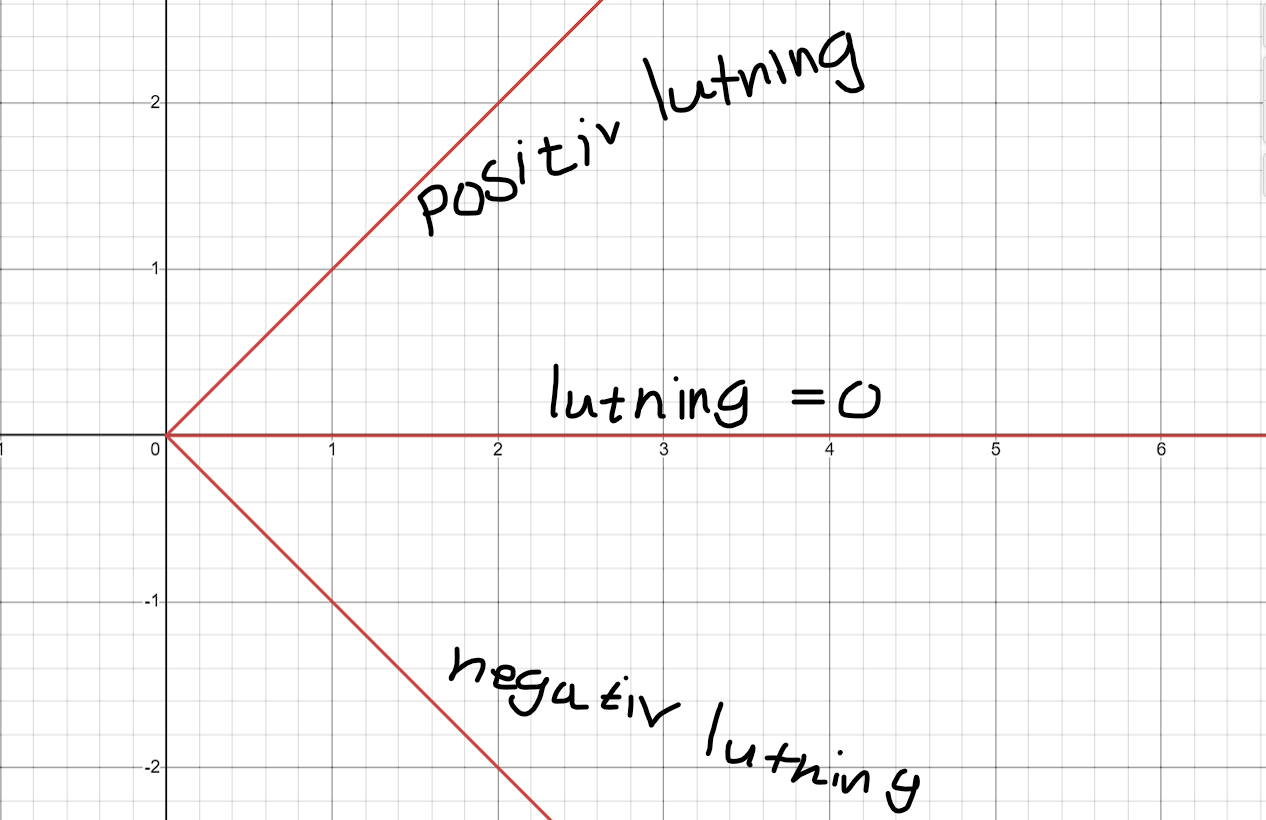
Jaha tack så mycket, nu förstår jag hur det funkar med backen!