Andraderivata - säkerhet: karaktär för extrempunkt
Tjenixen!
Har stött på en fundering enligt rubriken.
Med hjälp av andraderivatan kan man tydligen se karaktären för extrempunkten. Är f''(x) > 0 är det en minimipunkt. Är f''(x) < 0 är det en maximipunkt. Jag förstår inte hur man kan vara säker på detta.
Höger om en minimipunkt växer funktionen (& derivatan är positiv).
Höger om en maximipunkt avtager funktionen (& derivatan är negativ).
Vad missar jag? Hur kan andraderivatan visa karaktären, igenom enbart dess värde? Andraderivatan avslöjar ju inte funktionens värde vänster om extrempunkten?! Eller??
Mvh förvirrad rackare
För det första så behandlar vi ju extrempunkter, dvs. punkter där derivatan, f'(x)=0.
Betrakta funktionen f'(x) vars derivata är f''(x) i en av f:s extrempunkter.
Eftersom att det är en extrempunkt för f så passerar f' x-axeln i punkten i fråga, ty f'(x) skall vara 0. Detta kan den göra antingen genom att gå från ett negativt värde till ett positivt värde (vilket motsvarar att f':s derivata f''>0), eller att gå från ett positivt värde till ett negativt värde (vilket motsvarar att f':s derivata f''<0) eller att den nätt och jämnt tangerar 0-värdet.
Om f' går från ett negativt värde till ett positivt värde så motsvarar detta att f:s derivata till en början är negativ, för att bli mindre och mindre negativ tills att den blir 0, för att därefter bli mer och mer positiv. Så f är till en början avtagande, för att sedan vara neutral, innan den blir mer och mer ökande. Detta motsvarar en minimipunkt.
Om f' går från ett positivt värde till ett negativt värde så motsvarar detta att f:s derivata till en början är positiv, för att bli mindre och mindre positiv tills att den blir 0, för att därefter bli mer och mer negativ. Så f är till en början ökande, för att sedan vara neutral, innan den blir mer och mer avtagande. Detta motsvarar en maximipunkt.
Hmm...
vilket motsvarar att f':s derivata f''>0
vilket motsvarar att f':s derivata f''<0
Det är dessa två bitar jag inte hänger med på. Hur menar du? I självaste extrempunkten är derivatan noll. Varför blir, dömt genom värdet på f bis, det antingen max/min-punkt - enbart med värdet att döma???
f må ha en derivata som är noll, men det säger ingenting om f':s derivata.
Tänk dig att du ritar upp funktion f' framför dig.
I den punkt som är extrempunkt till f(x), kalla den x0, så måste f'(x)= 0, dvs f'(x0)= 0.
Detta innebär att f' passerar x-linjen i den punkten.
Om den passerar x-linjen genom att gå från ett negativt värde, t.ex. -1, till ett positivt värde, t.ex. 1 så har vi en funktion som blir större och större. Om den blir större och större är det en positiv derivata. Så funktionen f'(x) har alltså en positiv derivata i punkten x0. f':s derivata är f'', så man kan även skriva detta som att f''(x0)>0.
Om den passerar x-linjen genom att gå från ett positivt värde, t.ex. 1, till ett negativt värde, t.ex. -1 så har vi en funktion som blir mindre och mindre. Om den blir mindre och mindre är det en negativ derivata. Så funktionen f'(x) har alltså en negativ derivata i punkten x0. f':s derivata är f'', så man kan även skriva detta som att f''(x0)<0.
Detta innebär att f' passerar x-linjen i den punkten.
Hur kommer detta sig?
Förlåt, x-axeln.
Detta kommer sig av att f(x0) är en extrempunkt, så f'(x0)= 0, och om man ritar upp f' som en funktion i en graf så blir det precis på x-axeln. x-axeln markerar ju hur som x sträcker ut sig och man utgår från origo, på samma sätt som hur y-axeln markerar hur som y sträcker ut sig och man utgår även där från origo. X-axeln ligger där y=0 och y-axeln där x=0.
Ursäkta om jag lägger mig i, take it or leave it.
Med teckenschema kan man kasta ljus över detta.
Förutsättningar: f(x) har derivatan f’(x).
f’(a) är noll (detta är viktigt, annars ger andraderivatatestet ingenting) och f’’(a) < 0.
Funktionerna är “snälla”, de har inga mysko hopp eller liknande.
Påstående: f(a) är maximum
“Bevis”
Teckenschema
x: a
f’’: – – –
f’: avtar 0 avtar
f’: + 0 –
f: växer Max avtar
Förklaring rad 2: eftersom f’’ är negativ i a är den negativ även i en omgivning till a.
rad 3: f’ avtar alltså i den omgivningen.
rad 4: Eftersom f’(a) = 0 så kommer f’ vara positiv till vänster och negativ till höger om a.
rad 5: Teckenväxlingen för f’ ger att f(a) är maximum.
Mogens:
Förklaring rad 2: eftersom f’’ är negativ i a är den negativ även i en omgivning till a.
Varför då?
Du har även skrivit " f' " två gånger -
f’: avtar 0 avtar
f’: + 0 –
Vad betyder detta, att det avtar både sidor om f', men på nästa rad är (för samma f') den + till vänster om; och till höger om: -
Bedinis:
och om man ritar upp f' som en funktion i en graf så blir det precis på x-axeln
Jag är ännu inte med på varför f(x0) äro på x-axeln? Hur menar du - hittar du på att den korsar x-axeln för situationens skull?
Sorry var borta en stund.
Redigerat:
f’’ är negativ för x = a. Då måste det finnas åtminstone en liten liten omgivning till a där f’’ är negativ, f’’ kan inte bara hoppa direkt till 0 (jag förutsatte att f’’ var kontinuerlig).
FELSKRIVET NEDAN RÄTTAT NU
Ja, jag skrev f’ två gånger. Först konstaterar jag att f’ avtar till vänster om a, att f’(a) är 0, och att f’ fortsätter att avta till höger om a. Alltså måste f’ vara positiv till vänster och negativ till höger om a.
När du hoppar i vattnet från trampolinen minskar ditt avstånd till bassängbotten, du passerar vattenytan och avståndet till botten fortsätter att minska. Alltså befann du dig över vattnet innan och under vattnet efter det att du passerade vattenytan.
Inte helt lätt men helt logiskt :)
Angående "lägger sig i": absolut inga problem. Det väsentliga är att den som frågar får hjälp, och mina förklaringar gav tydligen inte tillräckligt.
Angående f(x0) på x-axeln: Ingenstans har jag sagt att f(x0) hamnar på x-axeln. Det jag sagt är att x0 är en extrempunkt, vilket gör att dess derivata, f'(x0), är noll. Så om man ritar upp funktionen f'(x) (som råkar vara funktionen f:s derivata men det är ovidkommande) så kommer den bli 0 i punkten x0, vilket motsvarar att den ritas ut på x-axeln, för på x-axeln är y=0.
Hej igen
Återkopplar på papper denna gång. Återkom om det är svårt å tyda!

Grjejen, Bedisins, är väl att du gett nog med hjälp, men det går inte in i min förståelse, trots det. och det beror på något jag inte kan urskilja!
Du är tveksam kring varför funktionen f som har en derivata i x0 på 0 inte säger någonting om derivatans derivata.
Betänk funktionen f(x)= x2. I punkten x=0 är derivatan 0, men andraderivatan 2.
Betänk funktionen f(x)= -x2. I punkten x=0 är derivatan 0, men andraderivatan -2.
Betänk funktionen f(x)= x3. I punkten x=0 är derivatan 0, men andraderivatan 0.
Ovan har du exempel på tre funktioner som alla stämmer in på beskrivningen "vi har en extrempunkt då x=0". Denna information var inte nog för att kunna säga om andraderivatan i punkten var positiv, 0 eller negativ, så att bara säga att det är en extrempunkt där säger ingenting om andraderivatans utseende.
Sedan är det det här med att "passera x-axeln" - jag kanske skulle använt mig av en annan formulering eftersom du hänger upp dig på det, men det jag vill komma fram till är att derivatan i extrempunkten är 0, så om man ritar upp derivatan som en funktion av x så kommer y-värdet i det som var extrempunkten i f-funktionen att bli 0. Och har den värdet 0 så befinner den sig på x-axeln.
Vi kan ju ta de tre funktionerna jag skrev ovan som exempel.
Derivatan av x2 är 2*x. Ritar man upp 2*x som funktion kommer man få en rak linje som skär genom origo, så den korsar x-axeln i extrempunkten.
Derivatan av -x2 är -2*x. Ritar man upp -2*x som funktion kommer man få en rak linje som skär genom origo, så den korsar x-axeln i extrempunkten.
Derivatan av x3 är 3*x2. Ritar man upp 3*x2 som funktion kommer man få en parabel med minimipunkten (0,0) så kurvan tangerar nätt och jämnt x-axeln i den punkten.
Nilsson skrev:Höger om en minimipunkt växer funktionen (& derivatan är positiv).
Höger om en maximipunkt avtager funktionen (& derivatan är negativ).
Ja. Detta betyder med andra ord att derivatans derivata är positiv. Detta därför att förändringen av förändringen går från negativ till positiv lutning.
Andraderivatan avslöjar ju inte funktionens värde vänster om extrempunkten?! Eller??
Det den avslöjar är förändringen av förändringen eller derivatans derivata eller, enkelt, andraderivatan.
Se nedan bild:
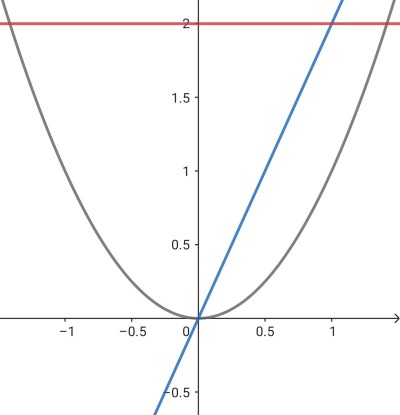
Funktionen (grå linje) går från att ha negativ lutning till att ha positiv lutning för ökande värde på x. Detta betyder att derivatans (blå linje) förändring är positiv. Detta betyder att andraderivatan (röd linje) måste vara positiv.
Varför? Jo, för att förändringen av förändringen är i en positiv riktning för ökande x och andraderivatan är per definition förändringen av derivatan.
Bedisins
 Har jag tänkt rätt?
Har jag tänkt rätt?
SaintVenant:
Ja. Detta betyder med andra ord att derivatans derivata är positiv. Detta därför att förändringen av förändringen går från negativ till positiv lutning.
Förändringen - d v s höger om extrempunkten?
Ok. Din visualisering hjälpte mig nog. Den röda linjen - hur ska man tolka den, den är ju horisontell.
Nilsson skrev:Har jag tänkt rätt?
Du har räknat ut första- och andraderivatan rätt för samtliga funktioner, och fått fram rätt värde av dem då x=0. Att f''(0) ej behöver vara 0 beror på att funktionen f''(x) inte har någon extrempunkt då x=0, till skillnad från funktionen f.
Du ser nu också att alla de tre funktionerna kan sägas ha extrempunkt då x=0, för derivatan är då 0.
Detta motiverar det jag sade tidigare: "f må ha en derivata som är noll, men det säger ingenting om f':s derivata."
Nilsson skrev:
Den röda linjen - hur ska man tolka den, den är ju horisontell.
Man skall tolka den som att andraderivatan är konstant, att den är oföränderlig.
Observera också att den blåa f'-funktionen går genom origo, dvs. då x=0 är även f'=0, och att den därmed passerar x-axeln (som i grafen har värden mellan -1 och 1 markerade) då x=0.
Ok, tack för hjälpen!



