Ändra rekursionsformel så att vi får ungefärlig uppgift på roten ur 23. Konstig uppgift.
Talföljden an+1= 0,5(12an + an), a1 = 3 ger en följd av tal som ger ett allt bättre närmevärde till .
Hur ska vi ändra formeln om vi i stället vill ha ett ungefärligt värde på ?
Jag fattar inte, ska man bara kolla på hur rekursionsformeln se ut och lägga in 23 istället för 12 utifrån egen gissning? Jag gissade den delen rätt och det är det som står på facit, men jag fattar inte varför. Dessutom vet jag inte varför a1 = 4 på facit.
Kan jag få hjälp, tack.
Denna följd bygger på att ekvationen (om vi generaliserar till ett tal )
har lösningen
Notera att det talföljden gör är att ta (det aritmetiska) medelvärdet mellan
och
Genom att iterera detta får vi ett närmevärde som blir bättre och bättre. Om du är nyfiken på en bättre förklaring varför den fungerar kan du söka upp "Herons method" (Herons metod är ett specialfall av Newtons metod, vilket används approximera nollställen till funktioner)
AlexMu skrev:Denna följd bygger på att ekvationen (om vi generaliserar till ett tal )
har lösningen
Notera att det talföljden gör är att ta (det aritmetiska) medelvärdet mellan
och
Genom att iterera detta får vi ett närmevärde som blir bättre och bättre. Om du är nyfiken på en bättre förklaring varför den fungerar kan du söka upp "Herons method" (Herons metod är ett specialfall av Newtons metod, vilket används approximera nollställen till funktioner)
Tack.
Men vet någon varför a1 är 4 och inte 5? På en video av Fredrik förklarar han det genom att säga att roten ur 23 är mellan kvadraten av 4 och kvadraten av 5. Men han förklarar inte varför just 4 och inte 5?
Studenten06 skrev:Men vet någon varför a1 är 4 och inte 5? På en video av Fredrik förklarar han det genom att säga att roten ur 23 är mellan kvadraten av 4 och kvadraten av 5. Men han förklarar inte varför just 4 och inte 5?
Det spelar inte jättestor roll. Båda kommer mycket snabbt konvergera mot . 5 är faktiskt bättre eftersom 5 är närmare än 4. Men med en mycket liten marginal.
Såhär blir processen om vi börjar med 4: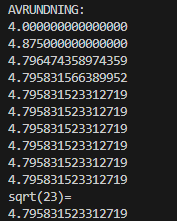 Om vi börjar med 5:
Om vi börjar med 5:

Som du ser går det mycket snabbt i båda fallen att komma fram till med 15 decimalers precision!
Så här stor blir differensen mellan dem, alltså finns det praktiskt taget ingen skillnad när vi har gjort några iterationer
Också, till och med om man börjar på typ 100 går det mycket snabbt att komma ned till rätt approximation!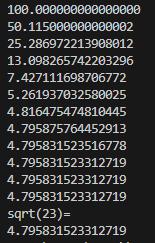
AlexMu skrev:Studenten06 skrev:Men vet någon varför a1 är 4 och inte 5? På en video av Fredrik förklarar han det genom att säga att roten ur 23 är mellan kvadraten av 4 och kvadraten av 5. Men han förklarar inte varför just 4 och inte 5?
Det spelar inte jättestor roll. Båda kommer mycket snabbt konvergera in mot . 5 är faktiskt bättre eftersom 5 är närmare än 4. Men med en mycket liten marginal.
Såhär blir processen om vi börjar med 4:Om vi börjar med 5:
Som du ser går det mycket snabbt i båda fallen att komma fram till med 15 decimalers precision!
Så här stor blir differensen mellan dem, alltså finns det praktiskt taget ingen skillnad när vi har gjort några iterationer
Wow! Tack.




