Ändlig eller oändlig integral?
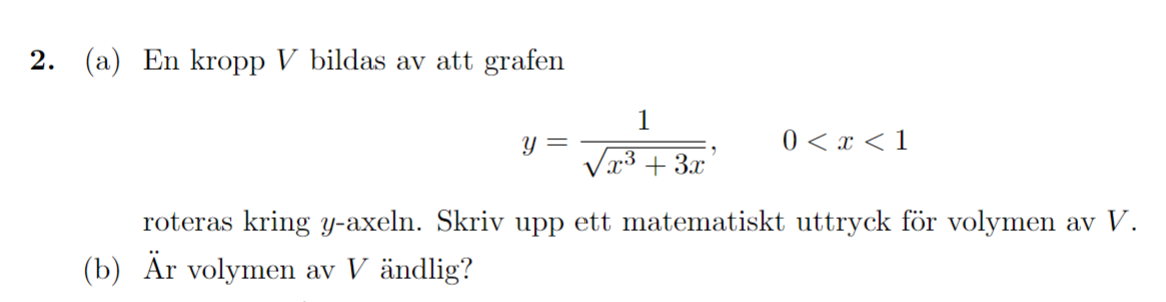
Hej! Jag har kört fast på fråga 2b). Jag tänker att man kan jämföra integralen med en annan större integral som är lättare att integrera på intervallet och se om den är konvergent eller ej, dvs enligt Kauchys integralkriterium. Problemet är att jag inte riktigt vet vilken lämplig integral jag kan testa med. Någon som kan hjälpa?
Hur har du gjort på a-uppgiften?
Om inte den hade funnits så hade det varit smidigast att börja med en uppskattning uppåt, t ex slopa 3x för att göra nämnaren mindre och fknen större. Omvänt om du bilvisningarna divergens. Men ger inte resultatet på a också svaret på b?
Tomten skrev:Hur har du gjort på a-uppgiften?
Om inte den hade funnits så hade det varit smidigast att börja med en uppskattning uppåt, t ex slopa 3x för att göra nämnaren mindre och fknen större. Omvänt om du bilvisningarna divergens. Men ger inte resultatet på a också svaret på b?
Njae inte riktigt då avaret på a är integral vars primitiva funktion är mycket svår att lösa, jag tönker attan kanske kan jämföra den toerande funktionen y med en annan roterande funktion f(x)= 1/x
Den är intejättesvår för när du använder ”skivformeln”då kvadrerar du y så att rotmärket försvinner. Sedan gör du partialbråks uppdelning och får standard integraler. Prova får du se.
Tomten skrev:Den är intejättesvår för när du använder ”skivformeln”då kvadrerar du y så att rotmärket försvinner. Sedan gör du partialbråks uppdelning och får standard integraler. Prova får du se.
Kvadreringen gör man väl om den roterar kring x, nu roteras den kring y och då kvaderares ej funktionen
Aj då, det såg jag inte. Men gör den rotationen så får vi se hur den integralen ser ut.

