Analysera krets med en kondensator

Jag har i uppgift att skriva en formel för V_c(t) för kretsen nedan, men har lite svårt för hur man ska analysera kretsen för att ställa upp ekvationerna, och vilka intervall man vill betrakta. I uppgiften anges att switchen har varit öppen länge, och att den stängs vid t = 0.

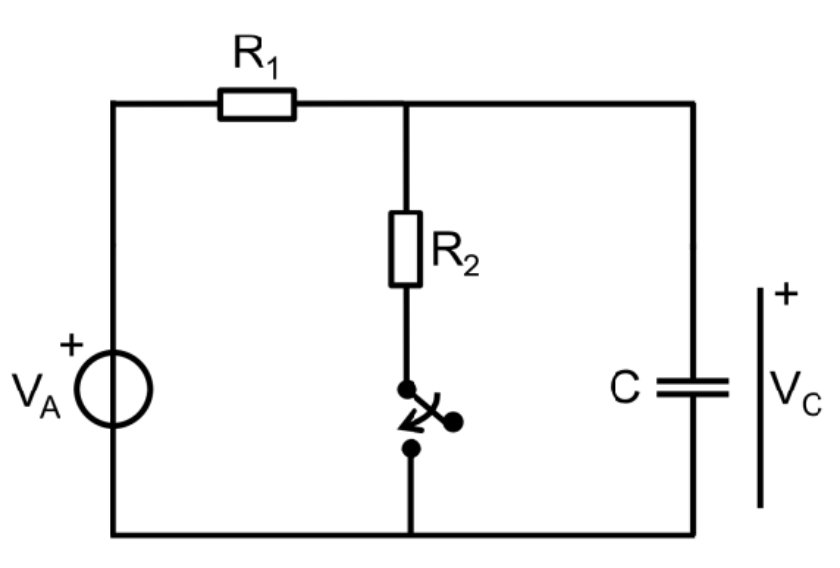
Jag påbörjade min lösning med att betrakta kretsen då t < 0. I detta fall har man en krets med 3 komponenter V, R₁ och C samt en gemensam ström I. Då t < 0 får jag fram följande:

V_A = V₁ + V_c (V₁ är potentialen över R₁)

= R₁ * I + V_c

Sedan resonerar jag att eftersom switchen varit öppen länge så borde C inte leda någon ström och därför blir V_A = V_c .

Nästa steg blir att analysera kretsen då t > 0, och det är här jag har lite svårt förstå hur man vill göra. Vill man dela upp detta intervall till t = 0 och t → $\infty$ ?

Jag tänker att efter ett tag (t → ∞) så borde potentialen över R₂ att vara ekvivalent med V_c.

Men precis då switchen stängs så kommer strömmen förgrenas och då får man istället att V_c = V_c(t). Kan man anta att potentialen över R₂ är samma som över C i detta fall, alltså V_c(t)? Har svårt att se hur ekvationen för detta fall kan ställas upp.

wedan skrev:
Har svårt att se hur ekvationen för detta fall kan ställas upp.

Det som efterfrågas är en differentialekvation. Ström är proportionell mot derivatan av laddningen i kondensatorn.

Ja så mycket har jag förstått. Strömmen genom kondensatorn C kan man skriva som I_c = C * $\frac{d V_{C}}{d t}$ .

I en exempeluppgift har man direkt applicerat:

V_c(t) = V_c(∞) + (V_c(0) - V_c(∞)) * $e^{- t / τ}$ där $τ$ = R_eq * C

Om jag använder denna formel (som verkar vara vedertagen) räcker det att hitta R_eq, V_c(0) samt V_c(∞).

R_eq = R_TH = R₁ + R₂

För V_c(0) resonerar jag att eftersom V_c är kontinuerlig så kommer V_c(0) = V_c(t < 0), alltså V_c(0) = V_A

För V_c(∞) så ser man att när kondensatorn slutar leda ström så kommer V_c = V_R2 . Eftersom R₁ || R₂så får jag genom spänningsdelning att V_R2= (V_AR₂ ) / (R₁ + R₂ ).

Instoppat i den generella formeln blir alltså:

V_c(t) = $\frac{V_{A} R_{2}}{R_{1} + R_{2}} + (V_{A} - \frac{V_{A} R_{2}}{R_{1} + R_{2}}) * e^{(\frac{- t}{(R_{1} + R_{2}) * C})}$

Som jag förstått det kan är det ok att använda den generella formeln förutsatt att man hittar R_eq för kretsen

Tillägg: 14 apr 2025 19:06

Rättelse:

R_TH= $\frac{R_{1} R_{2}}{R_{1} + R_{2}}$

wedan skrev:
Instoppat i den generella formeln blir alltså:

V_c(t) = $\frac{V_{A} R_{2}}{R_{1} + R_{2}} + (V_{A} - \frac{V_{A} R_{2}}{R_{1} + R_{2}}) * e^{(\frac{- t}{R_{1} + R_{2}})}$

Du har nog bara glömt kapacitansen i exponenten.

Sedan tror jag inte att RC-tiden är given av R₁ och R₂ i seriekoppling.

Ja den missade jag. Tack!

Jag förstår inte riktigt vad detta skulle innebära. Kan du utveckla?

Jag fick dessa värden genom att hitta Thévenin ekvivalenten där R_TH = R₁ + R₂och V_TH= V₂

Denna ekvation fick jag också fram i mitt första försök när jag använde KCL och Ohms lag, men hur går man vidare på enklast sätt? För att lösa differentialekvationen så tänker jag att jag vill jag ta fram den homogena differentialekvationen + partikulärlösningen. För den homogena får jag:

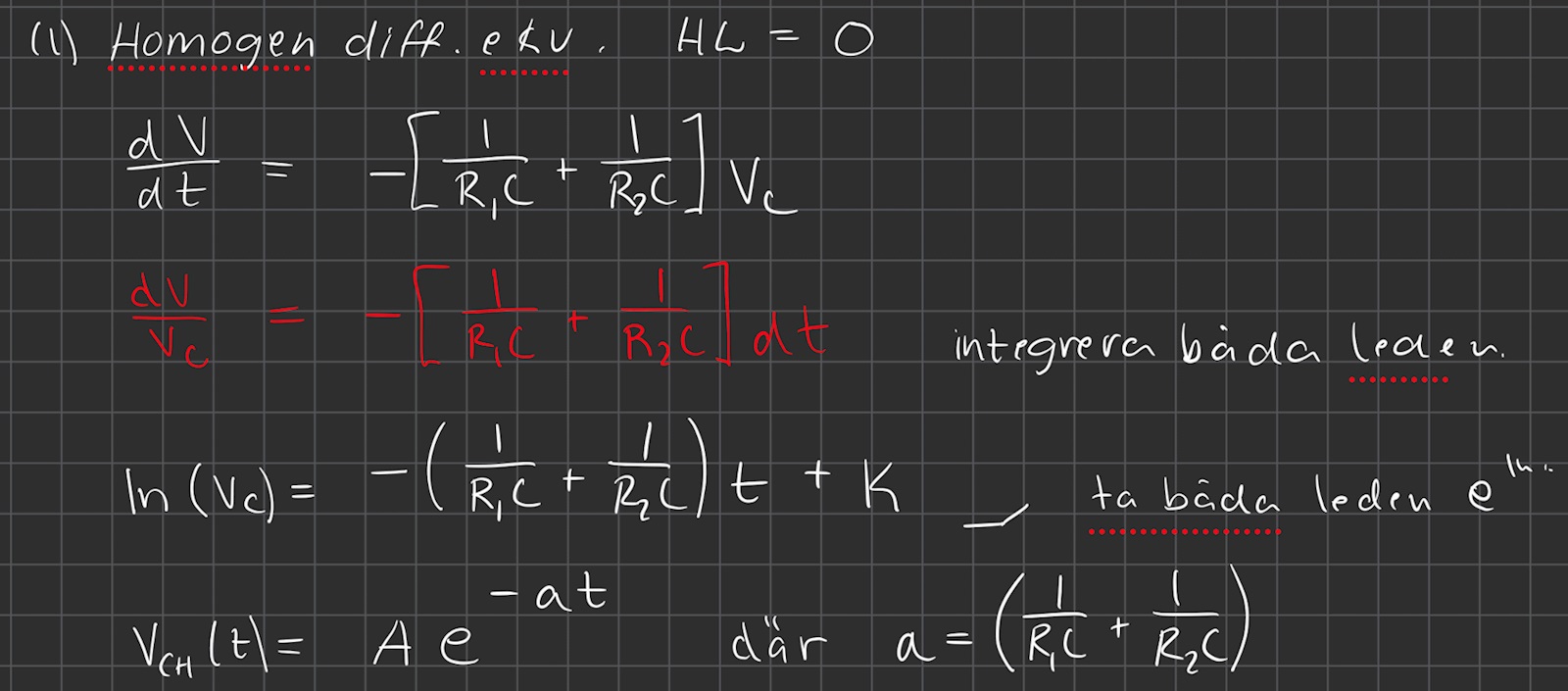
För partikulärlösningen får jag:

För att bestämma A så använder jag mig av begynnelsevillkoret att V_c(0) = V_A , och får då:

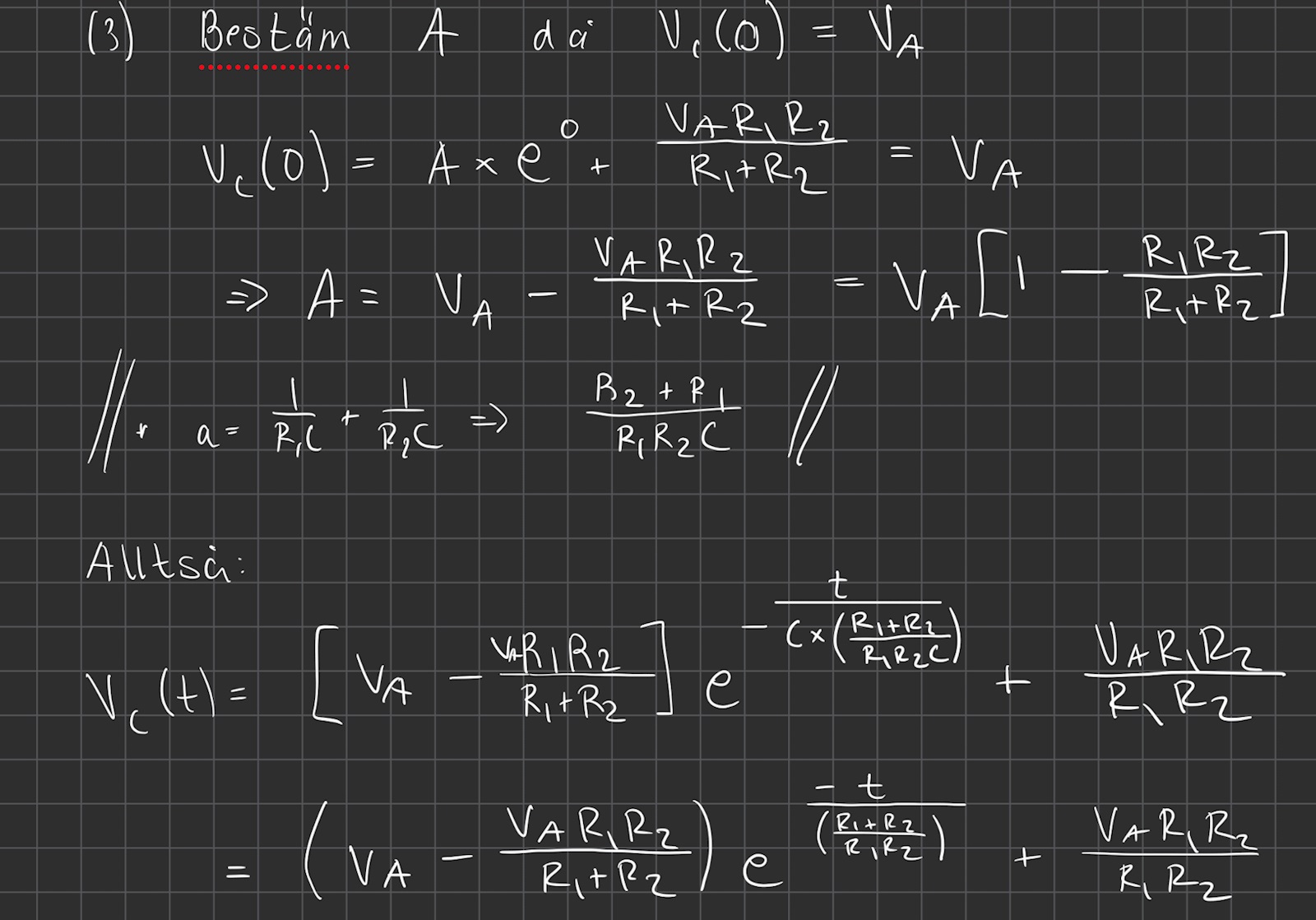
Vilket skiljer sig från min lösning med den "generella" formeln.

wedan skrev:
Vilket skiljer sig från min lösning med den "generella" formeln.

Rita spänningens värde som funktion av tid. Om de är lika, är det ingen skillnad. Om de är olika, se vilken kurva ger rätt värden.

Sambandet 0 + a•V_cp(t) = V_A/C

kan knappast stämma. V_cp(t) och V_A är spänningar, medan a är en frekvens och C en kapacitans.

Svara

Visa senaste svar