Analog elektronik, Beräkna strömen ix med superposition. (L.Bergström 5.9)
Hej har lite problem med följande fråga:
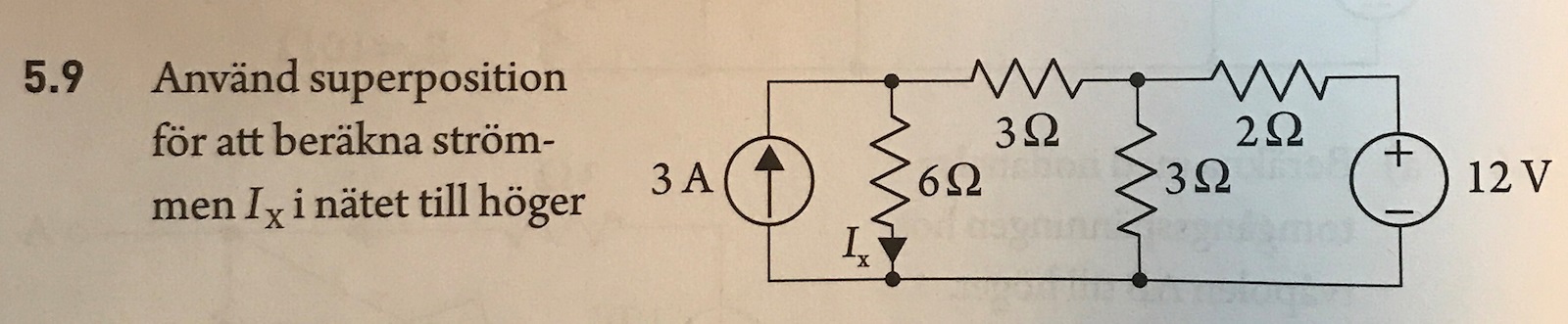
Där jag har gjort följande:
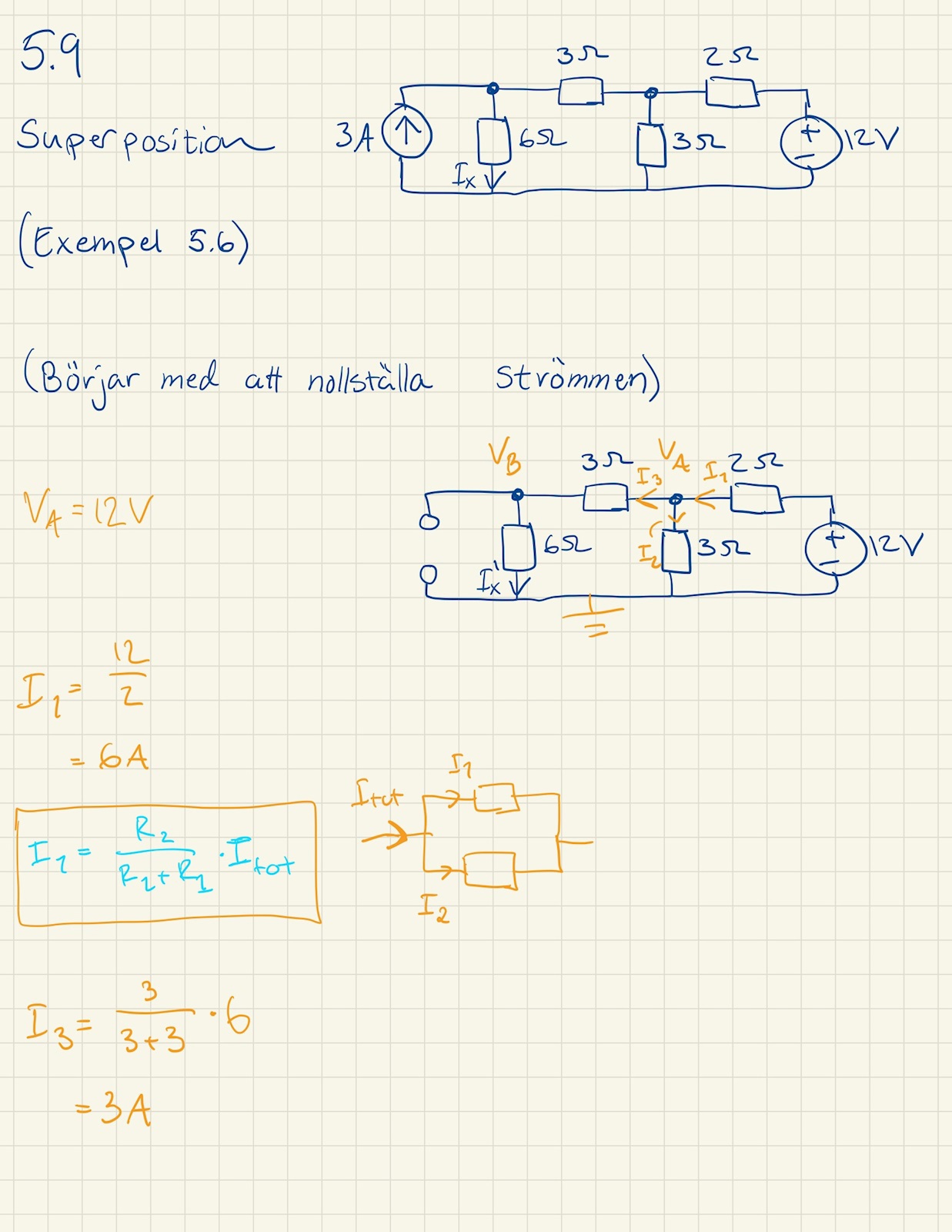
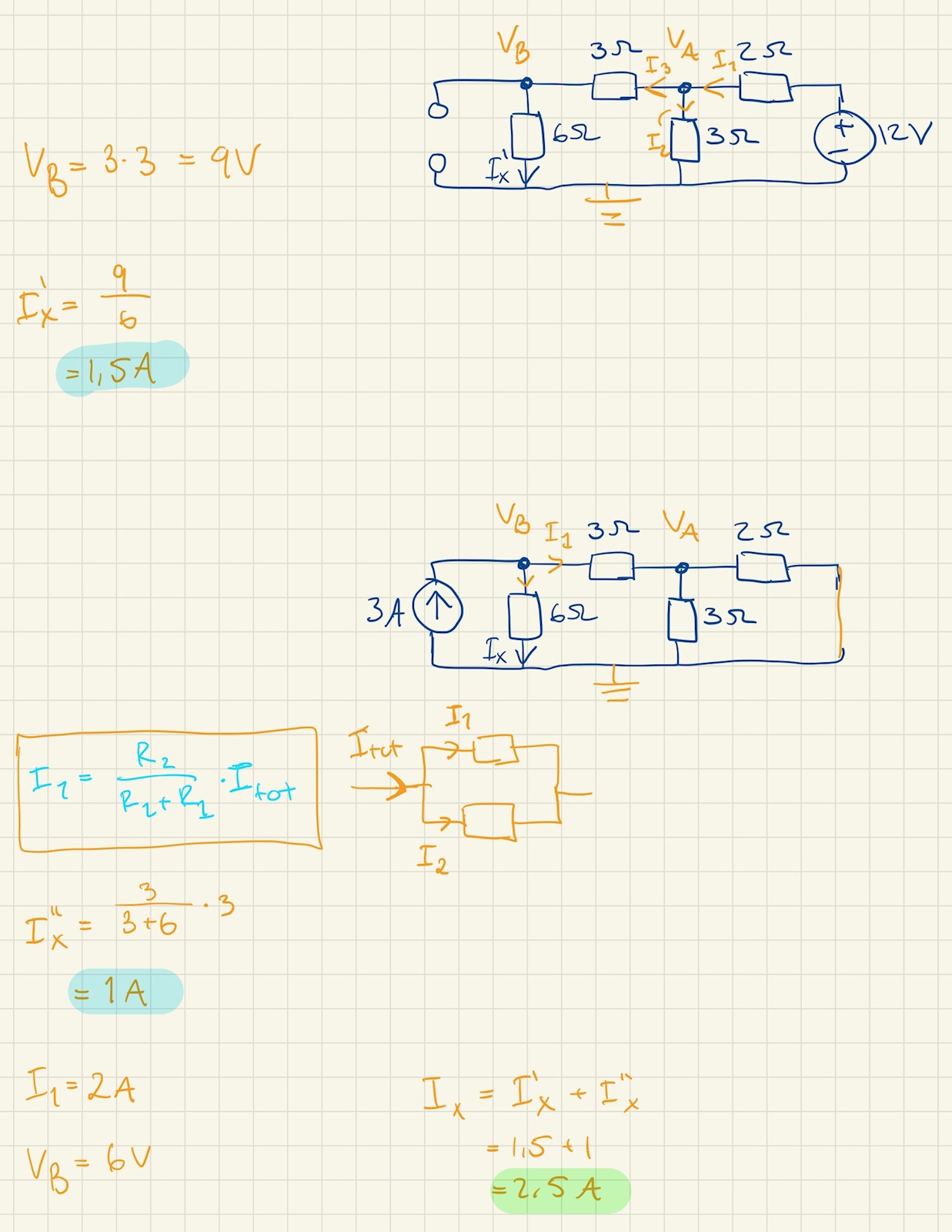
Men enligt facit så är svaret: 1,94A (1,234 + 0,706).
Jag har aldrig använt mig av superposition. Och det var ett tag sedan (så när som på trådarna du skapat på sistone där jag försökt vara hjälpsam) jag löste sånt här. Med denna brasklapp ur vägen, tror jag att du får fel redan då du sätter I1 till 6 A då du tagit bort strömkällan.
I det scenariot så kan man slå samman alla resistanserna till en enda ersättningsresistans kopplat till en spänningskälla á 12 V. Strömmen därigenom skall väl ges av Ohms lag, dvs. U= R*I.
De seriekopplade 3- och 6-Ohms-resistanserna (spänningen VB mittemellan dem) kan ersättas med en 9-Ohms-resistans. De därigenom uppkomna parallellkopplade 9- och 3-Ohms-resistanserna (spänningen VA före, 0 Volt efter) kan ersättas med en 9/4-Ohms-resistor. Därefter består kretsen av två seriekopplade resistorer med styrkan 2 respektive 9/4 Ohm, vilket ger 17/4 Ohm.
Ohms lag ger en ström på 12 Volt /(17/4) Ohm= 48/17 Ampere. Denna ström har inte fått någon möjlighet att dela upp sig förrän vid nodpunkten där spänningen är VA så I1 borde bli 48/17 eller 2,8235... Ampere.
Hummm, förstår inte hur 6 ohm och 3 ohms resistorerna är seriekopplade, i mina ögon är de parallellkopplade :/
(edit: ser nu att det inte var 9 ohm parallellt med 3 ohm)
Bedinsis skrev:Jag har aldrig använt mig av superposition. Och det var ett tag sedan (så när som på trådarna du skapat på sistone där jag försökt vara hjälpsam) jag löste sånt här. Med denna brasklapp ur vägen, tror jag att du får fel redan då du sätter I1 till 6 A då du tagit bort strömkällan.
I det scenariot så kan man slå samman alla resistanserna till en enda ersättningsresistans kopplat till en spänningskälla á 12 V. Strömmen därigenom skall väl ges av Ohms lag, dvs. U= R*I.
De seriekopplade 3- och 6-Ohms-resistanserna (spänningen VB mittemellan dem) kan ersättas med en 9-Ohms-resistans. De därigenom uppkomna parallellkopplade 9- och 3-Ohms-resistanserna (spänningen VA före, 0 Volt efter) kan ersättas med en 9/4-Ohms-resistor. Därefter består kretsen av två seriekopplade resistorer med styrkan 2 respektive 9/4 Ohm, vilket ger 17/4 Ohm.
Ohms lag ger en ström på 12 Volt /(17/4) Ohm= 48/17 Ampere. Denna ström har inte fått någon möjlighet att dela upp sig förrän vid nodpunkten där spänningen är VA så I1 borde bli 48/17 eller 2,8235... Ampere.
Hummm, okej... Vad bör strömmen vara för "strömskälle fallet" bör den vara negativ?
Jan Ragnar skrev:
Hej, vart kommer detta (se röd ring) ifrån? 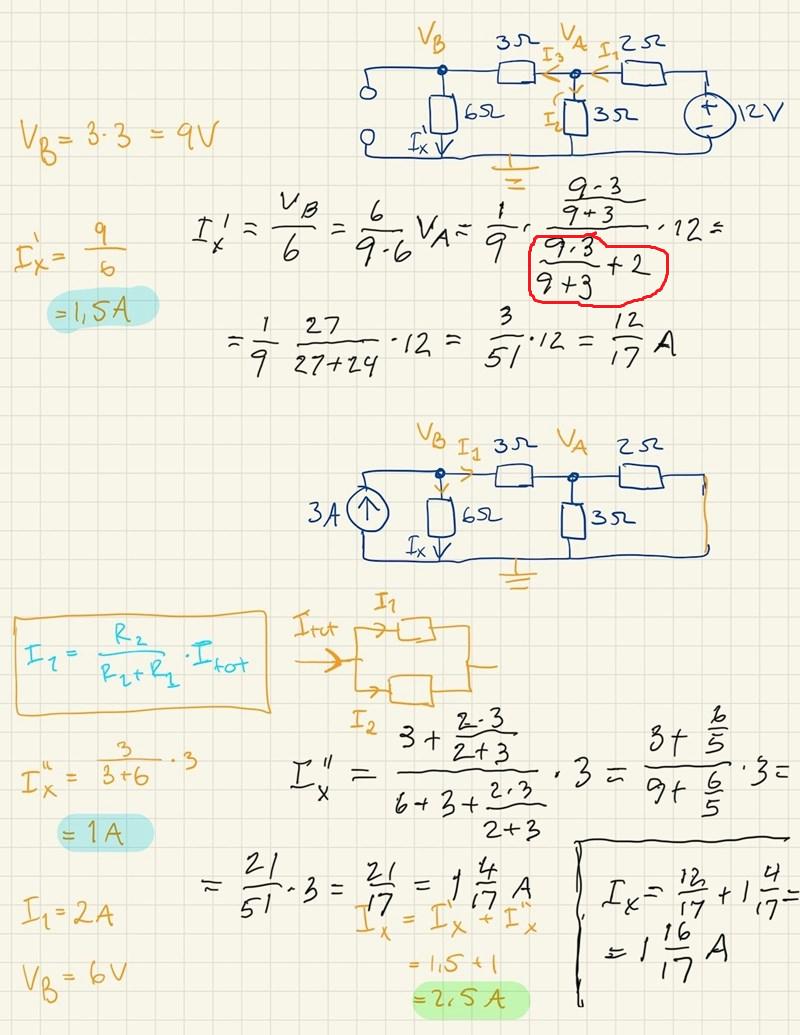
ChocolateTerrain skrev:Jan Ragnar skrev:
Hej, vart kommer detta (se röd ring) ifrån?
Formulerat i ord:
Spänningsfallet på 12 Volt i kretsen kan delas upp i två steg: ett spänningsfall över 2-Ohmsresistorn tills att spänningen blir VA Volt, och ett spänningsfall över ersättningsresistansen på de övriga resistorerna tills att spänningen blir 0 Volt.
Kvoten beskriver hur stor andel av spänningsfallet som sker över ersättningsresistansen.
VA=RersättRersätt+2*12
Hummmm, har försökt att förenkla kretsen mer får tyvärr fel svar... Är det fel att göra det eller har jag tolkat någon seriekoppling/parallellkoppling fel?
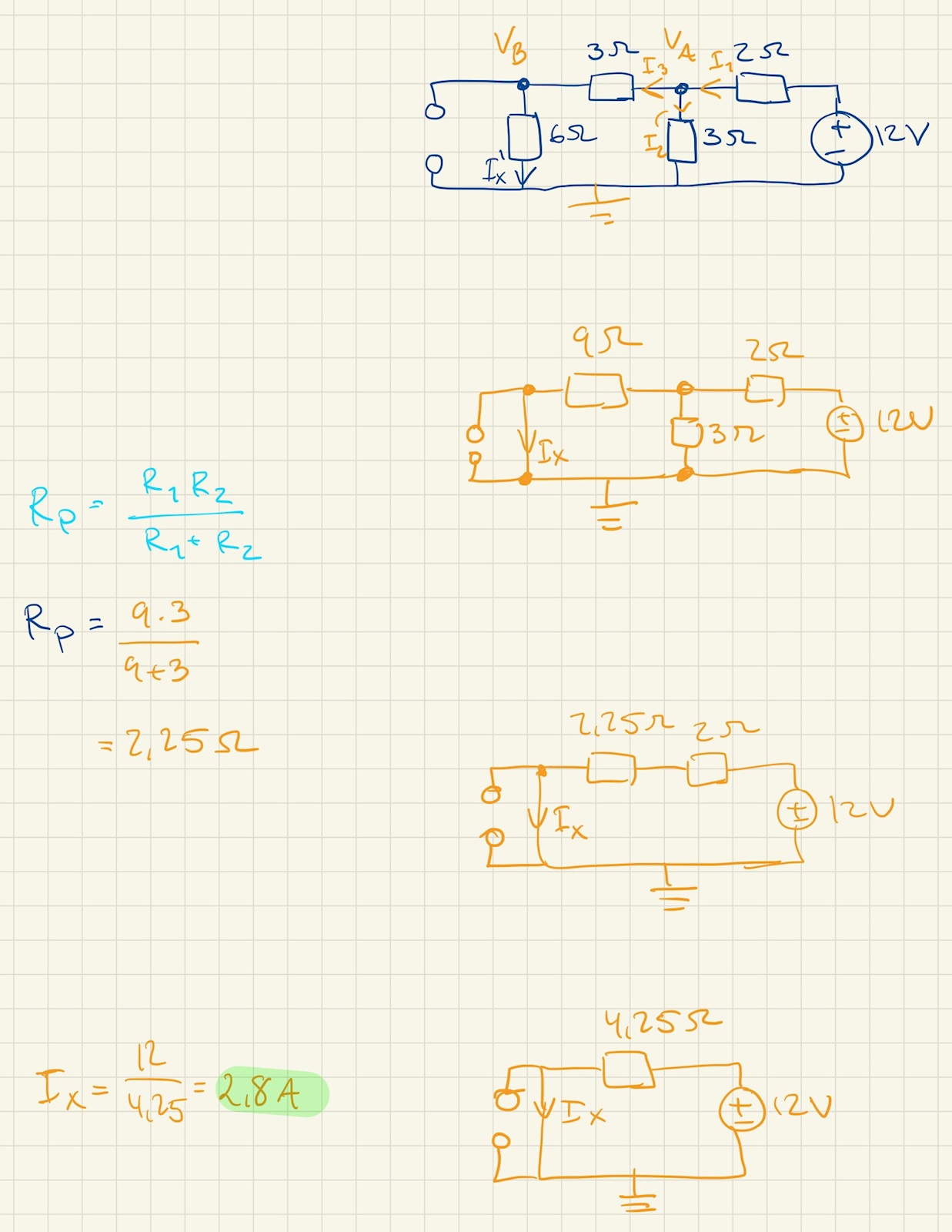
Du har tolkat den rätt, men du får fel då du tror att all ström i kretsen kommer att motsvaras av det som du kallat Ix'; detta kommer motsvara det som du i det inledande inlägget kallade I1.
Ahh.... Blir detta då också fel?
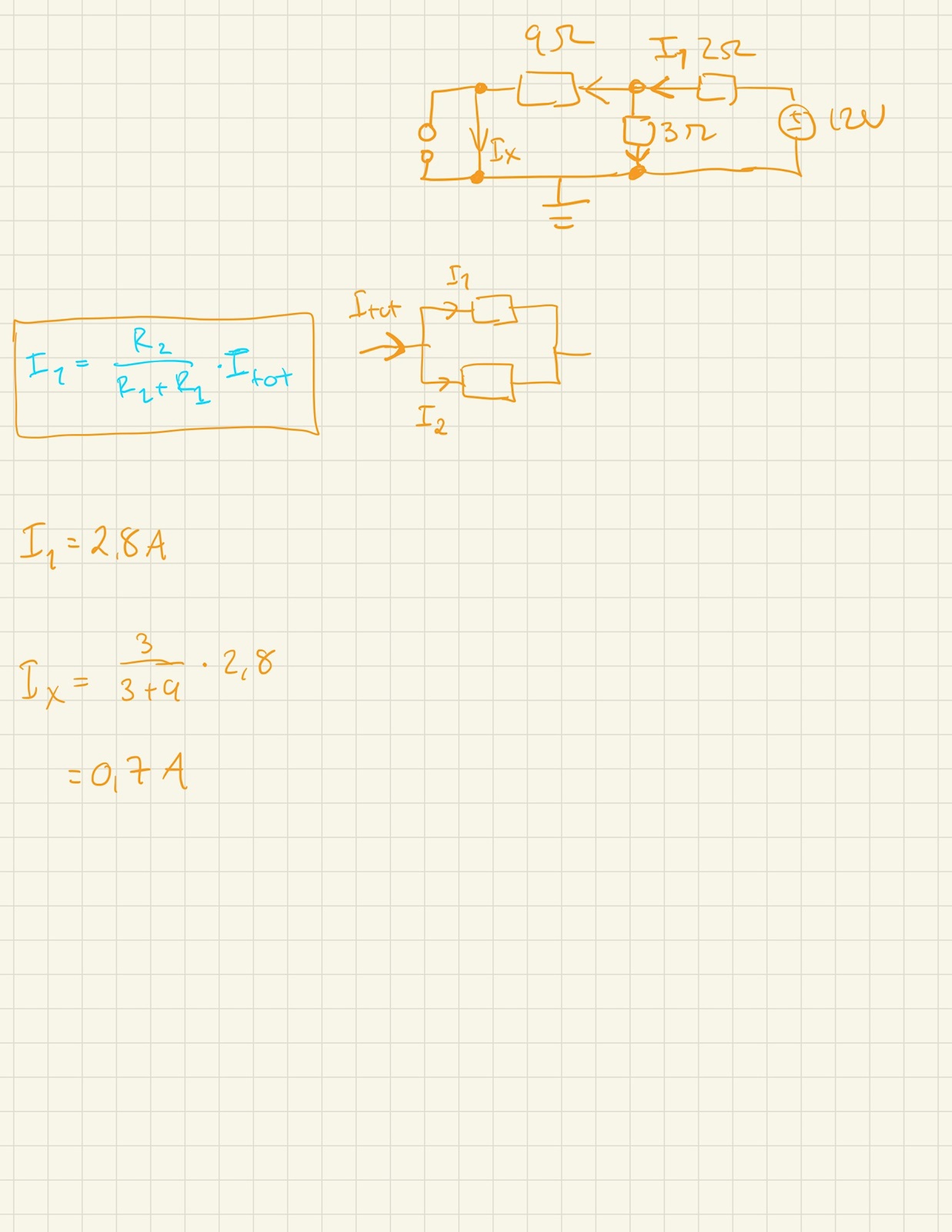
Nej, det blir rätt.
Se även Jan Ragnars uträkning i inlägg #7. Hen har fått samma svar. (12/17 = 0,70588235294...)
Aha! Men då undrar jag varför det är I1 och inte Ix, är det för att I1 är den enda ström som går genom alla resistorer?
Ja. Den delar upp sig i I2 och I3.
Okej, tack! Då antar jag att följande även stämmer: (då strömkällan är nollställd)
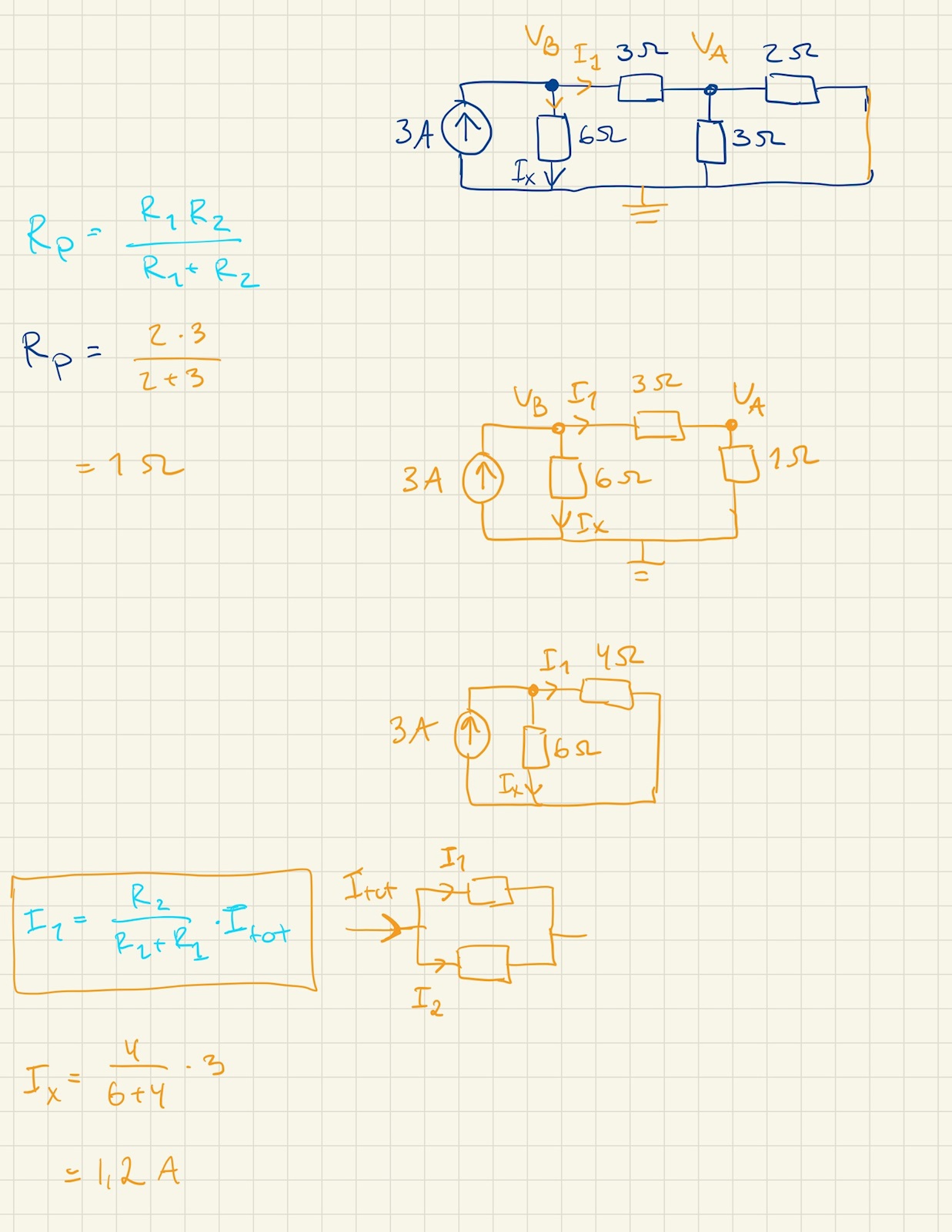
Hur får du ersättningsresistansen för de två parallellkopplade 2- och 3-Ohms-resistorerna att bli 1 Ohm?
Enligt följande:

Kan du visa den uträkningen? Det blir inte 1.
Ah.... nog tänkt lite för snabbt:
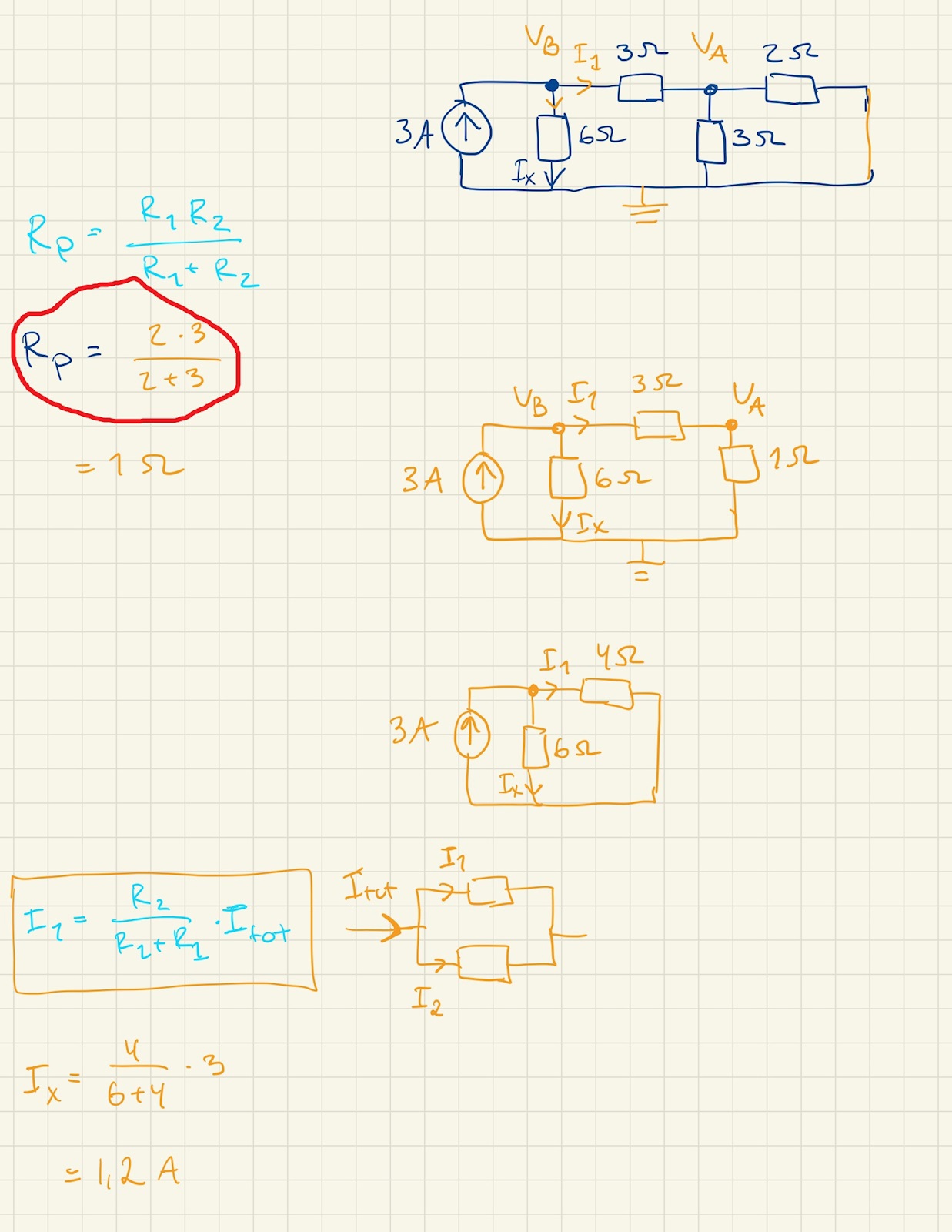
men ja Rp=2*32+3=1,2Ω
Ja.
Då är det väl bara att räkna på med din nya ersättningsresistans för att hitta Ix''.
Toppen! Tack!!!




