Analog elektronik, Beräkna momentanvärdesuttrycket för strömmen (komplexa metoden) (L.Bergström 9.2)
Hej! Har lite problem med följande uppgift:

Där jag har gjort följande:

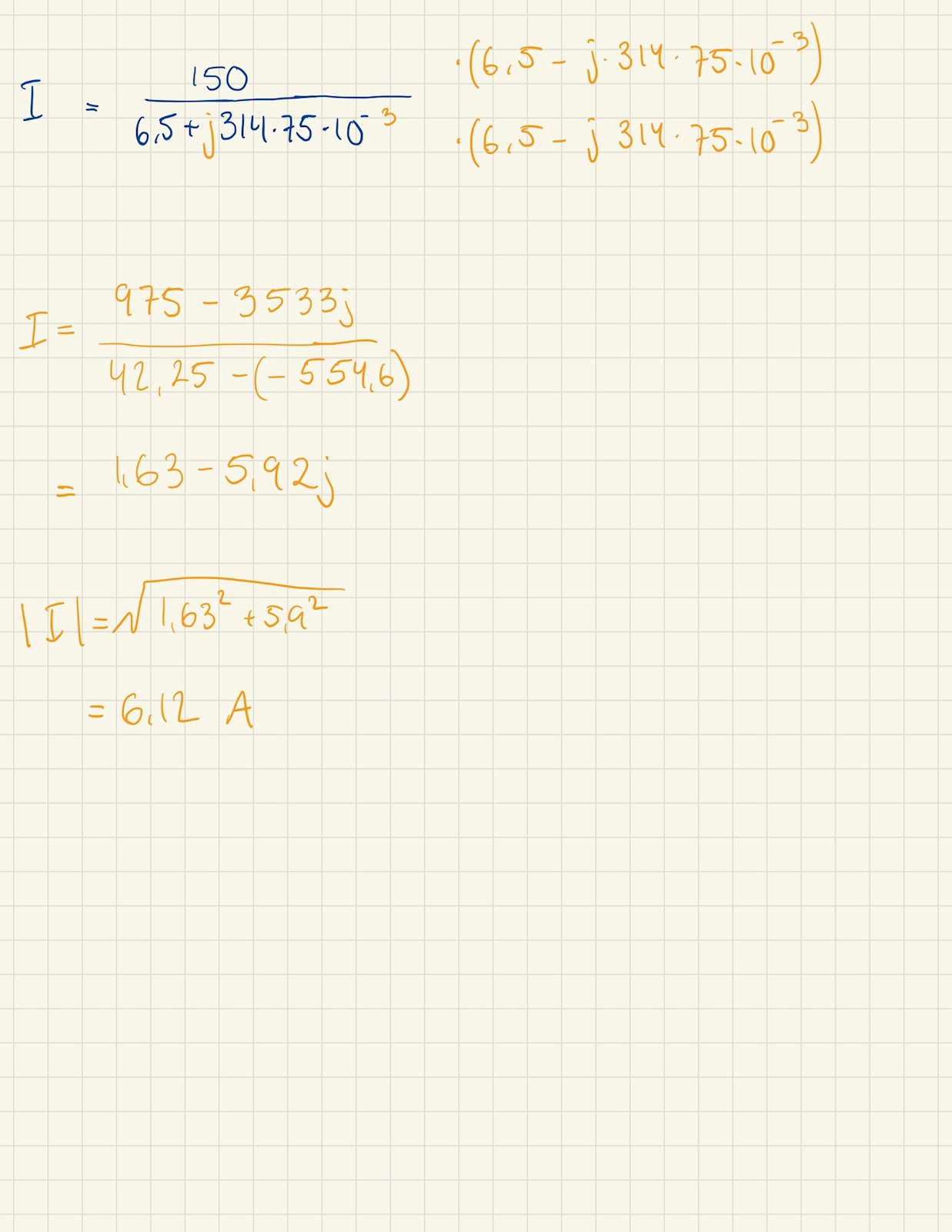
Men stämmer inte överens med facit, något som ser vad jag har gjort för fel?
Hej!
Det står i uppgiften att du ska beräkna uttrycket för momentanströmmen. Nu ser det ut som att du har beräknat rms-värdet istället (eftersom 150V polspänning måste vara ett rms-värde).
Har inte facit svarat med ett uttryck I=Asin(wt+fi) ?
Hummm.... Missat helt, men toppvärdet bör då vara 150*√2≈212V? Jo, facit har svarat i I=A*sin(ωt+α) men jag var osäker på att jag hade beräknat strömmen rätt så kollade facit och såg att jag hade gjort fel så skrev inte ut "svaret helt".
Spänningens toppvärde borde bli 212V som du skriver. Då borde toppvärdet på strömmen bli 8.7A. Stämmer det med facit?
Hej! Japp det gör det! Tack! :D
Däremot får jag inte tecknet på faskonstanten att bli riktigt rätt... Jag har gjort följande:

Som jag tolkar kursboken:

så borde faskonstanten vara +74,5 (medan facit menar på -74,6)
Det måste finnas någon mer sida i kursboken som förklarar hur fasvinklen beräknas, eller hur? Jag förstår ungefär hur du har beräknat a och b, men för att inte förvirra för dig så kan vi använda samma metod som ni har gått igenom.
(sidan som du klippt in visar hur spänningen ser ut över en ideal induktans om du vet hur strömmen ser ut. I din uppgift är det tvärtom, du ska beräkna hur strömmen ser ut när du vet hur spänningen ser ut. Men inklippet ger ledtråden att strömmens faskonstant borde vara negativ, eftersom spänningen ska ligga före strömmen)
Du kan representera spänningen som imaginärdelen av
u=212·ejωt
Den komplexa impedansen som spolen utgör blir
Z=6.5+23.55j=24.4·ej·74.6∘
Strömmen blir då
i=uZ=212·ejωt24.4·ej·74.6∘=8.7·ej(ωt-74.6∘)
Im{8.7·ej(ωt-74.6∘)}=8.7·sin(ωt-74.6∘)
Känner du igen det här sättet att räkna, eller har ni använt någon annan metod?
Känner tyvärr inte igen sättet att räkna som du skriver men skulle säkert kunna sätta mig in i det, men jag gjorde följande:

Lite som du säger i #7 så är det ju spänningen och inte strömmen så har väl egentligen blandat ihop dem/inte tänkt på det....
Skillnaden mellan uppgiften och teoridelen i din bok är att uppgiften beskriver en ickeideal induktans, dvs när det även finns en resistiv del i induktansen, så att fasskillnaden mellan ström genom induktansen och spänning över induktansen inte längre är 90 grader, utan en vinkel som ligger mellan 0 och 90 grader (ström och spänning ligger i fas om den resistiva delen av totala impedansen är mycket större än den induktiva delen.
Om vi jämför din uträkning med bokens teoridel så har du alltså räknat ut "u-före-i-fasskillnaden" som i boken är 90 grader. Jag kluddade lite i din bok nedan, och strök det som inte gäller för den ickeideala induktorn.

Det innebär att det du har räknat ut här:
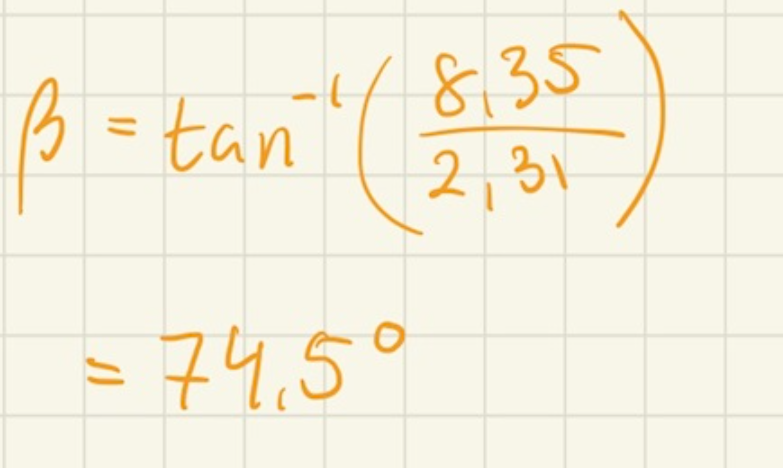
är inte β, utan "u-före-i-fasskillnaden".
Det innebär att teoridelens faskonstantformel blir:

och eftersom uppgiften säger att spänningens faskonstant är noll (αLi boken), så blir
0=β+"
Därifrån kommer minustecknet på faskonstanten. Och det kommer sig av att (som jag tror du redan förstått) att om spänningen ligger före strömmen så är det samma sak som att säga att strömmen ligger efter spänningen.
Jag känner att det blev förvirrande att försöka anpassa teoridelen för en ideal induktans till en uppgift med ickeideal induktans. Är du säker på att det inte finns beskrivet i din lärobok om hur man kan beskriva en godtycklig spänning, ström och impedans som komplexa tal på polär form, och sedan bara använda ohms lag och matematiska potenslagar på det?
Här är en ganska bra beskrivning https://wiki.sikvall.se/index.php/J%CF%89-metoden
hummm, jo det finns säkert i kursboken men är väl jag som inte förstått det, gissar på att det är något i stil med detta du menar: (speciellt b-uppg)


Använder väl egentligen inte riktigt som länken du skickade så kanske därför jag har lite problem med det....
Där har vi det! (Jo, det är samma sak som jag länkade till, bara att man använder lite olika notationer). Ovanstående måste du ägna tid åt att lära, jag lovar att du kommer inte att ångra dig på tentan!
Ställ frågorna här på PA, vi hjälper dig såklart!
Okej, tack för hjälpen! (och motivationen! :D)


