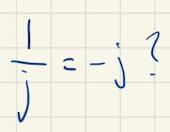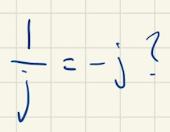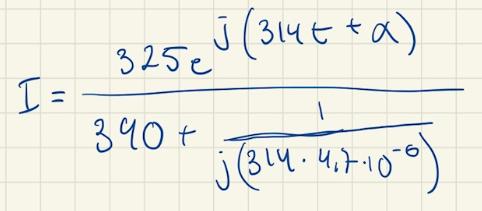Analog elektronik, Beräkna momentanvärdesuttrycket för strömmen (komplexa metoden) (L.Bergström 9.1)
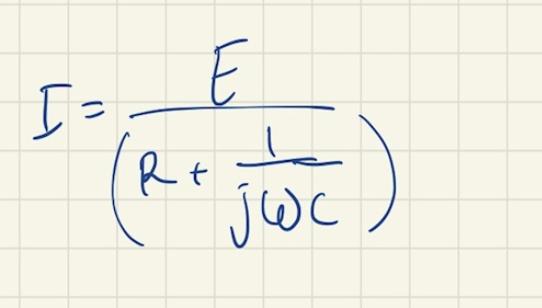
Hej! Har fastnat på följande uppgift (a-uppg):

Där jag har gjort följande:
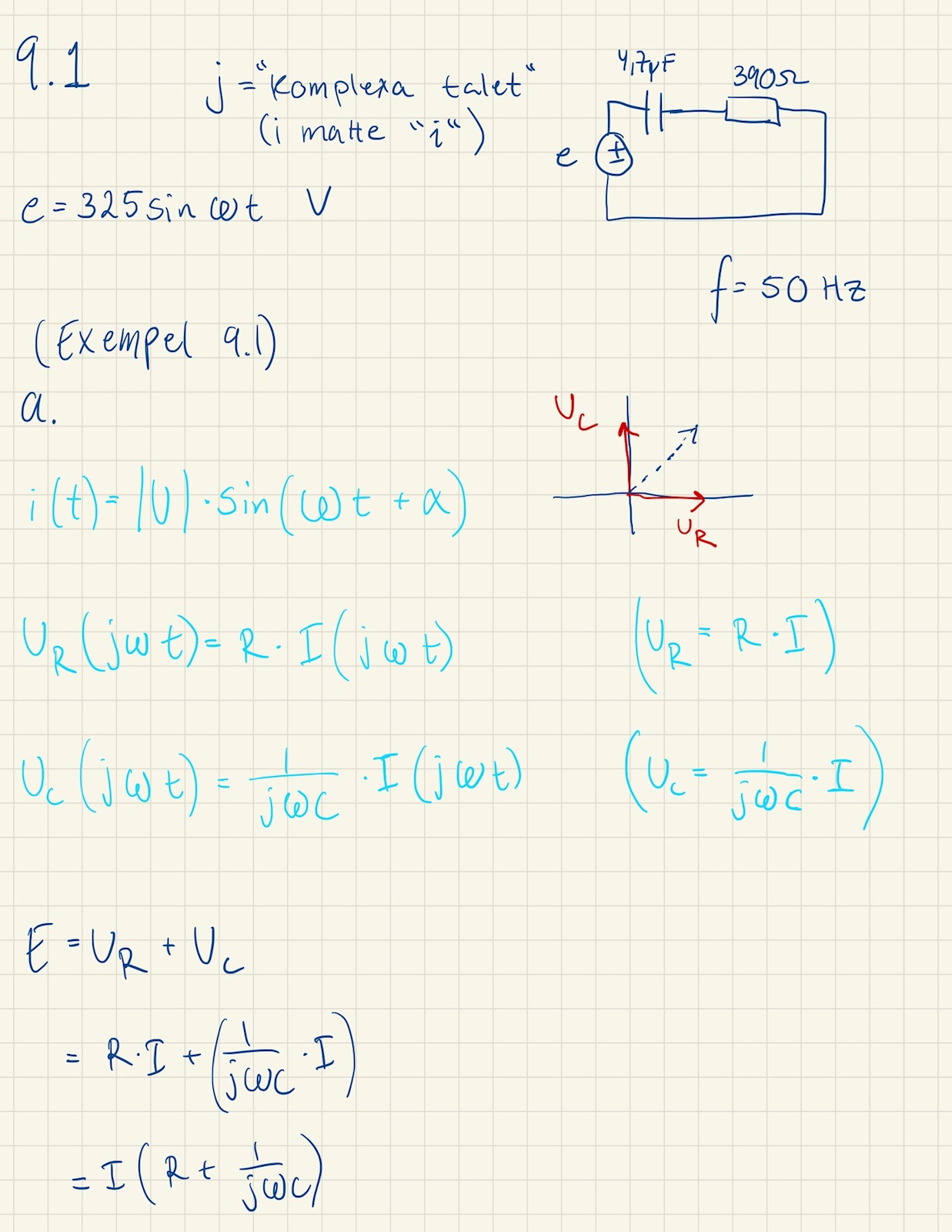
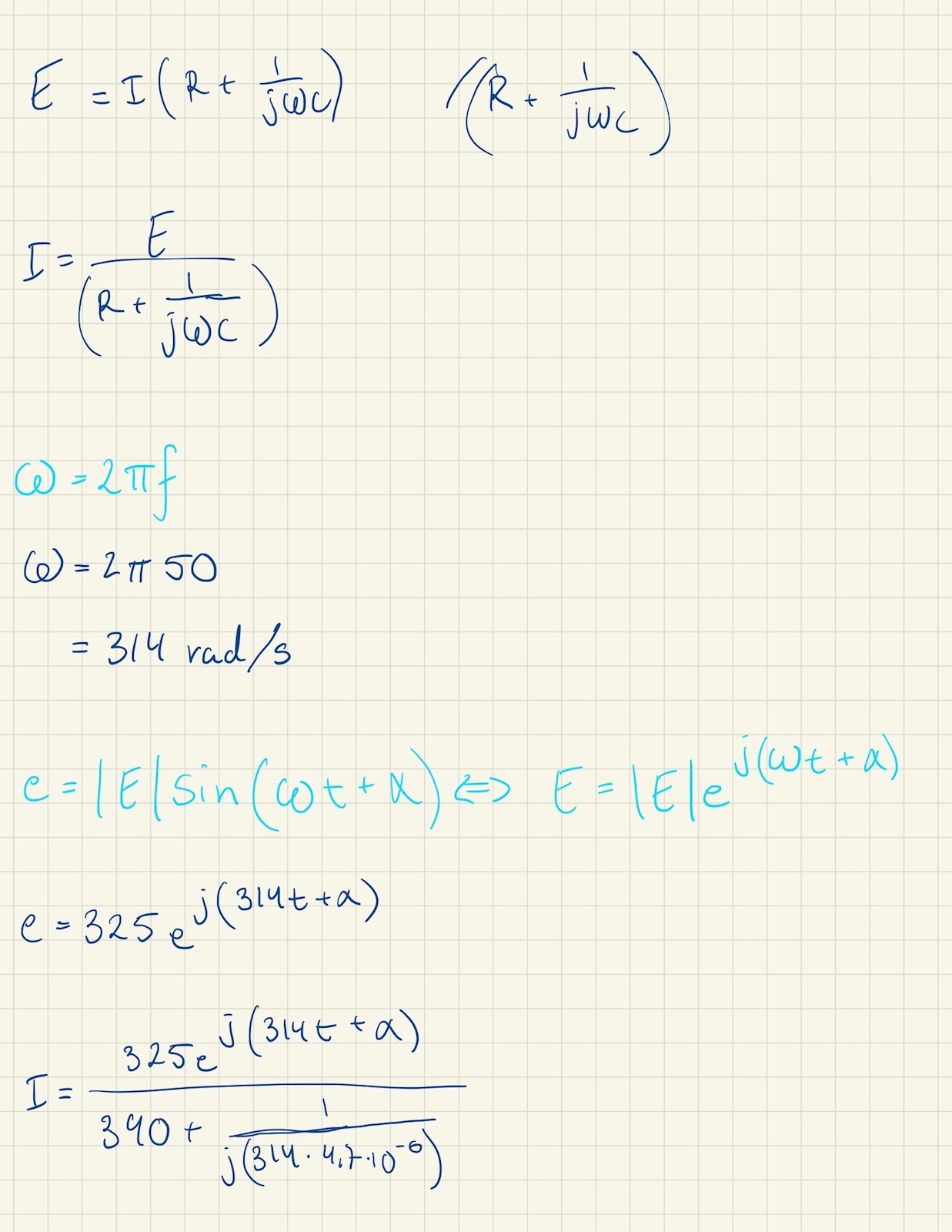
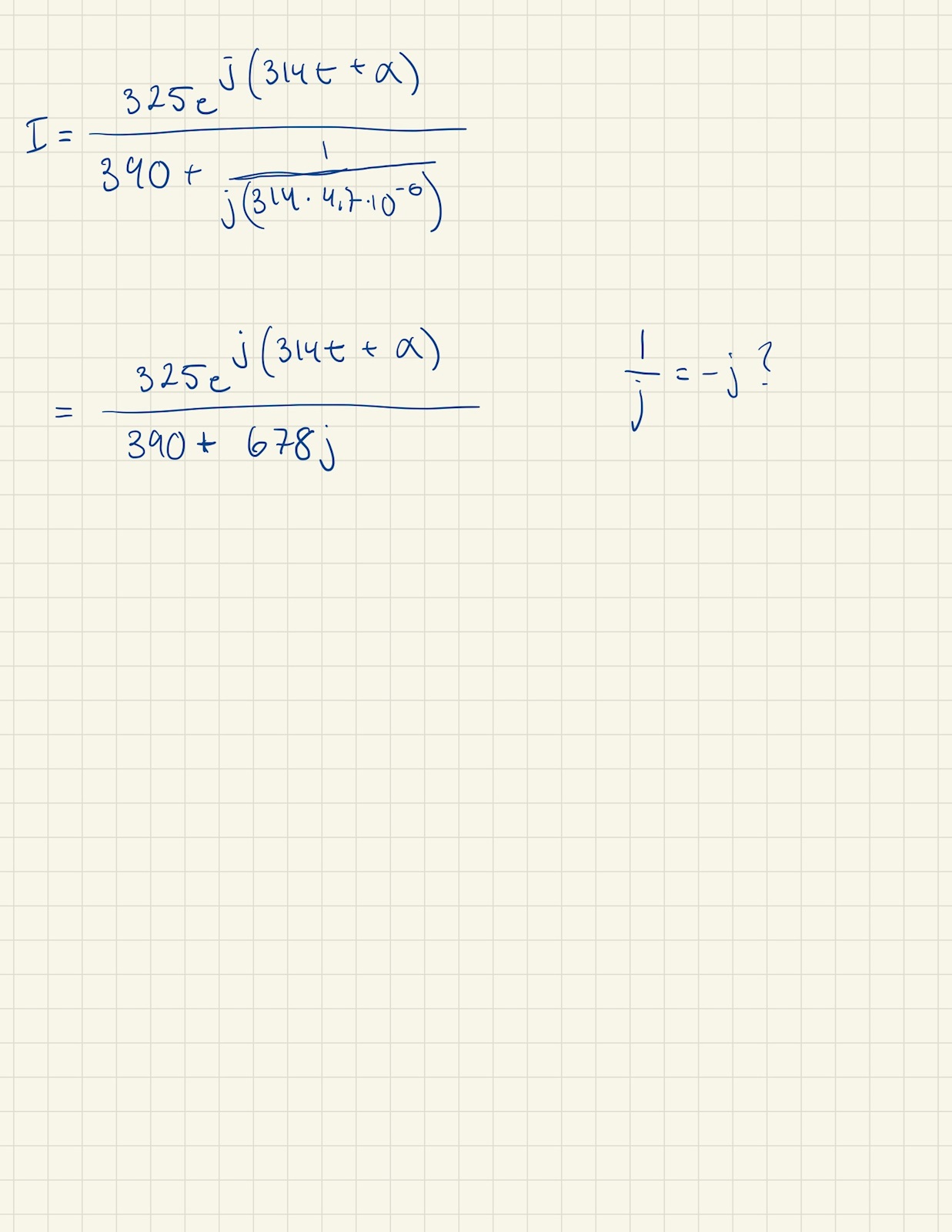
Där jag sedan kör fast och kommer tyvärr inte loss...
Jättebra början!
ChocolateTerrain skrev:
Ja precis! Varför? Jo för att .
Om du använder dig av det i denna uträkning (nämnaren):
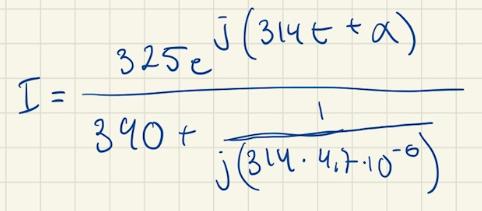
så får du inte

Vad får du i nämnaren?

Varför lägga in alfa här? Är det inte lättare att använda spänningen som referens?
Du blandar olika sätt att representera komplexa tal, det krävs att du får det på samma form.
Jag skulle föreslå att du fortsätter härifrån:
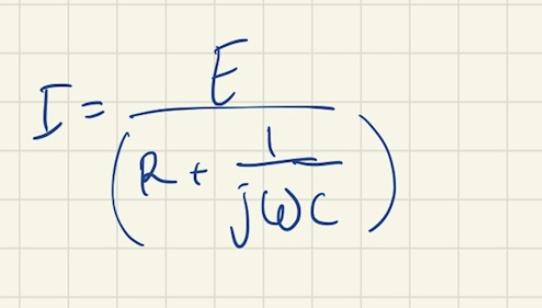
Till slut hamnar man i ett uttryck som liknar I = a + bj. Då får man amplitud och fasförskjutningen för strömmen ur detta.
Första steget: Multplicera täljare och nämnare med jwC
fner skrev:Jättebra början!
ChocolateTerrain skrev:Ja precis! Varför? Jo för att .
Om du använder dig av det i denna uträkning (nämnaren):
så får du inte
Vad får du i nämnaren?
Humm... gjorde två alternativ:

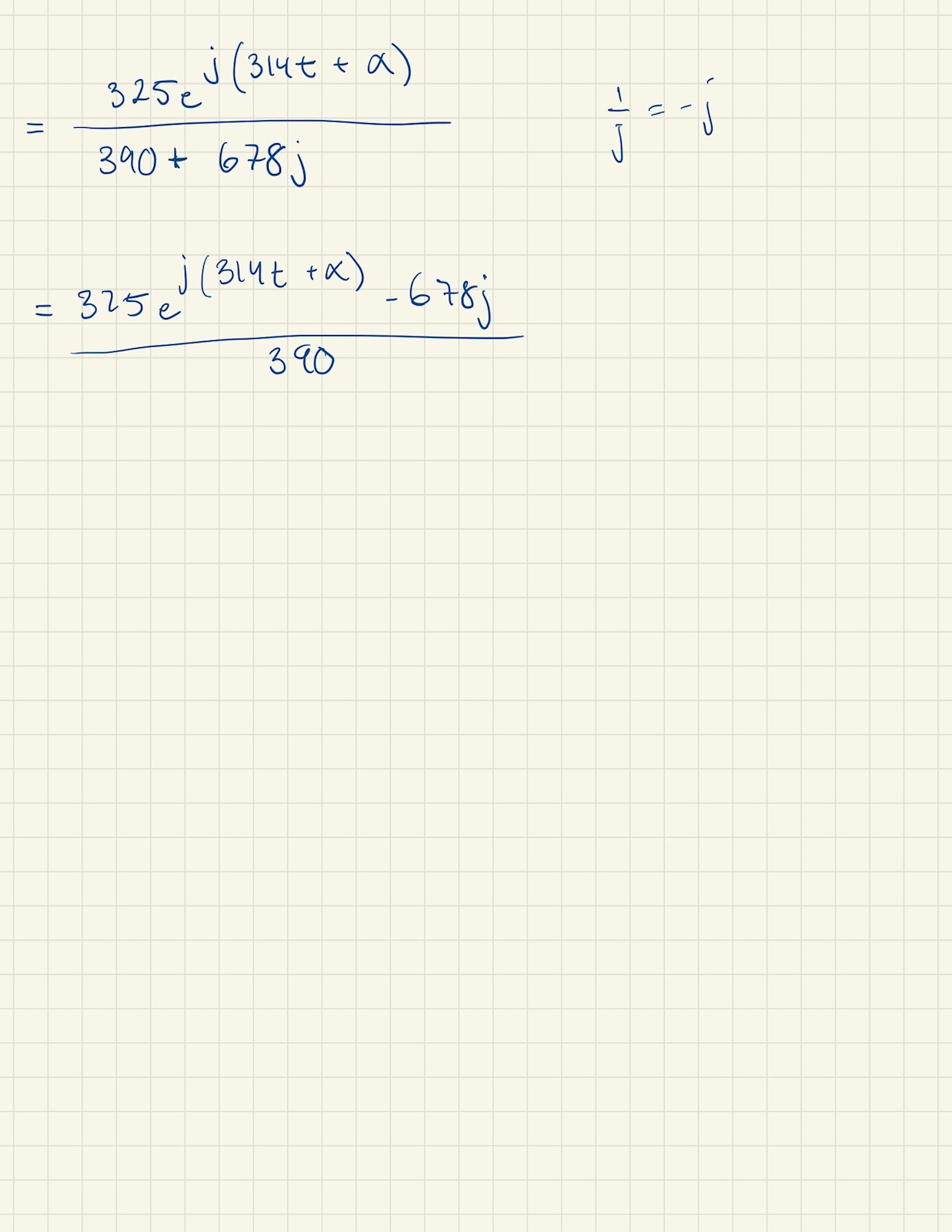
(vilket egentligen bör vara samma matematiska operation)
Som fner påpekade, det ska vara ett minustecken i nämnaren.
Ditt näst sista ark är rätt. Det sista arket är fel.
ThomasN skrev:
Varför lägga in alfa här? Är det inte lättare att använda spänningen som referens?
Du blandar olika sätt att representera komplexa tal, det krävs att du får det på samma form.
Jag skulle föreslå att du fortsätter härifrån:
Till slut hamnar man i ett uttryck som liknar I = a + bj. Då får man amplitud och fasförskjutningen för strömmen ur detta.
Första steget: Multplicera täljare och nämnare med jwC
Okej, gjorde såhär:
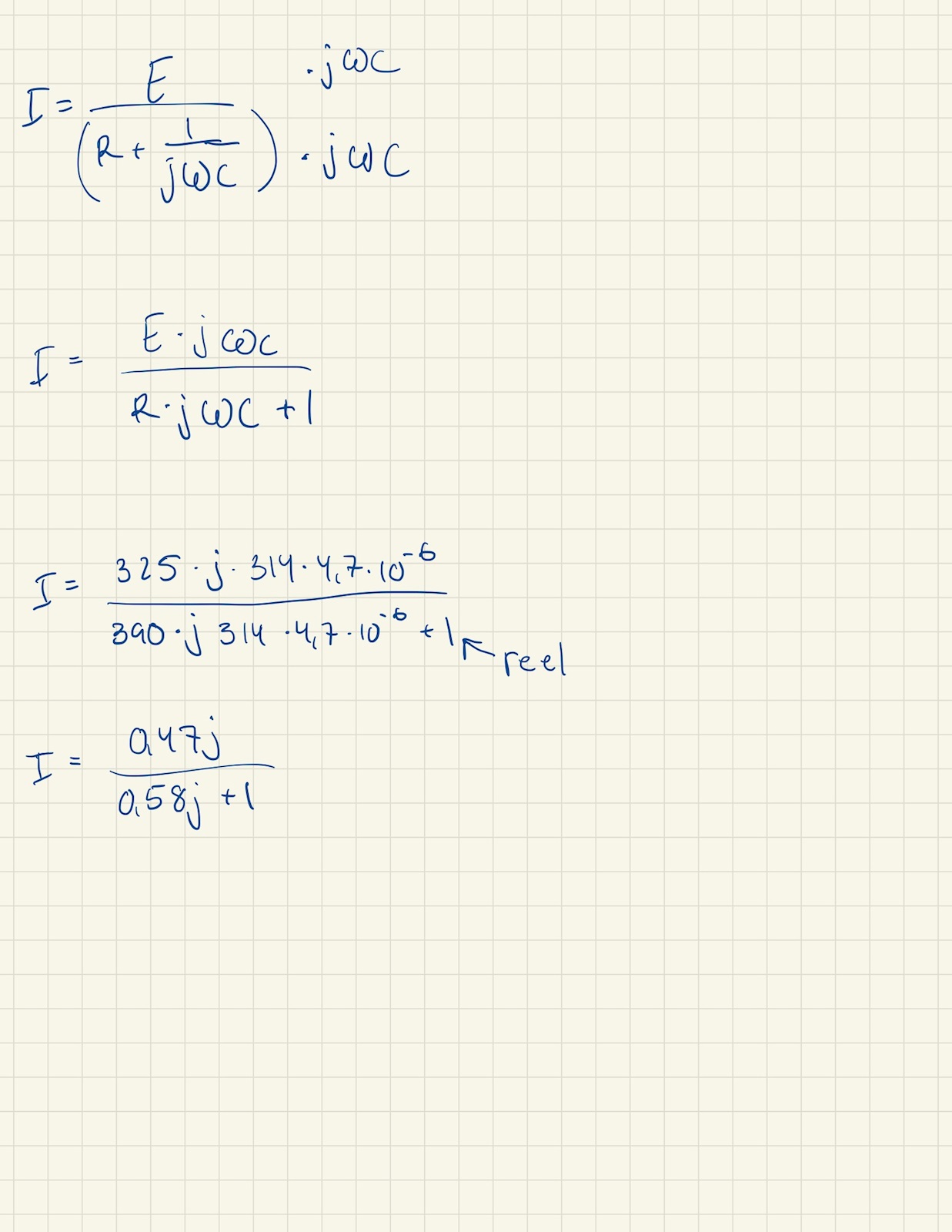
sen kom jag inte längre
Du är ju nära nu! Använd bara det komplexa konjugatet (tror jag det heter).
Dvs
Ahaaa!! Nu fick jag till det!
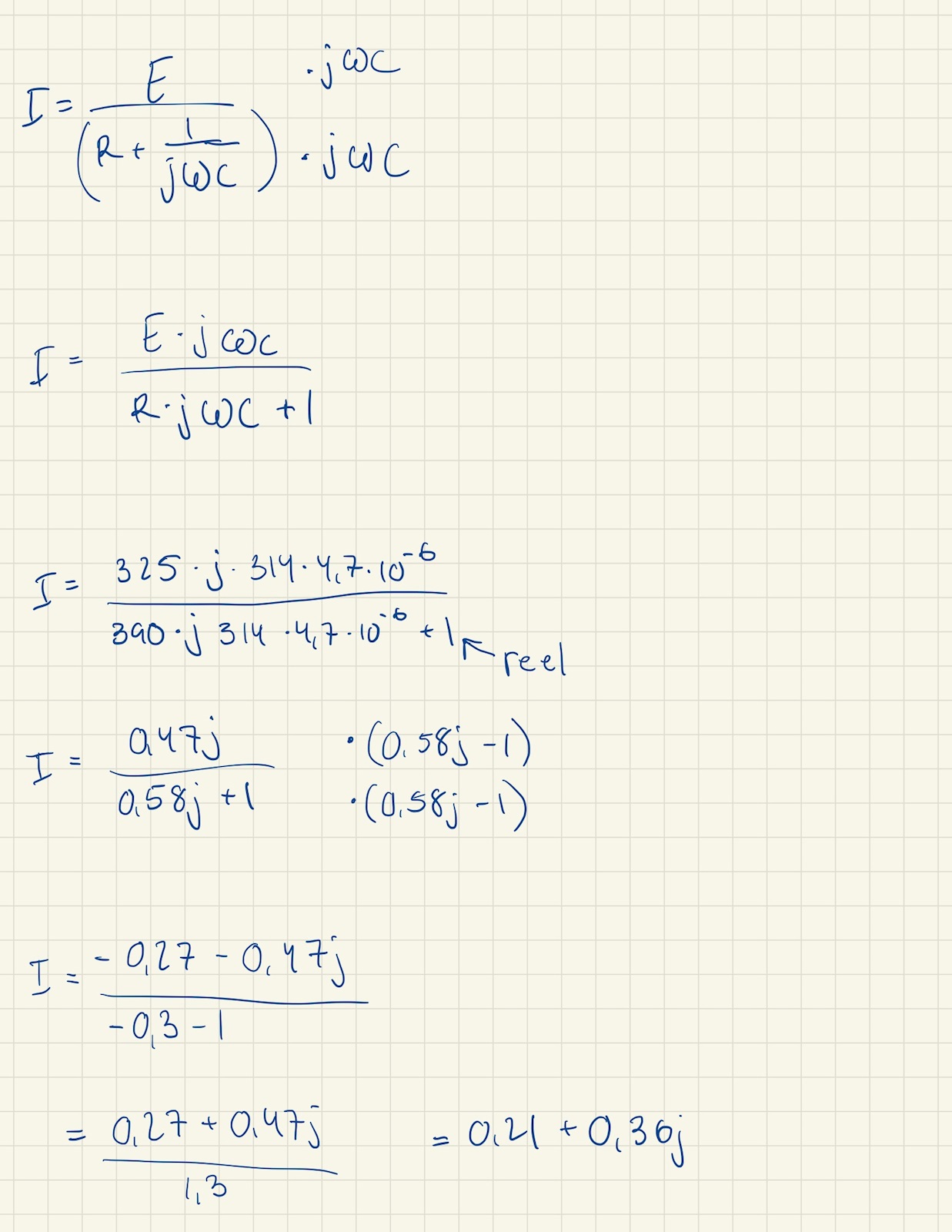
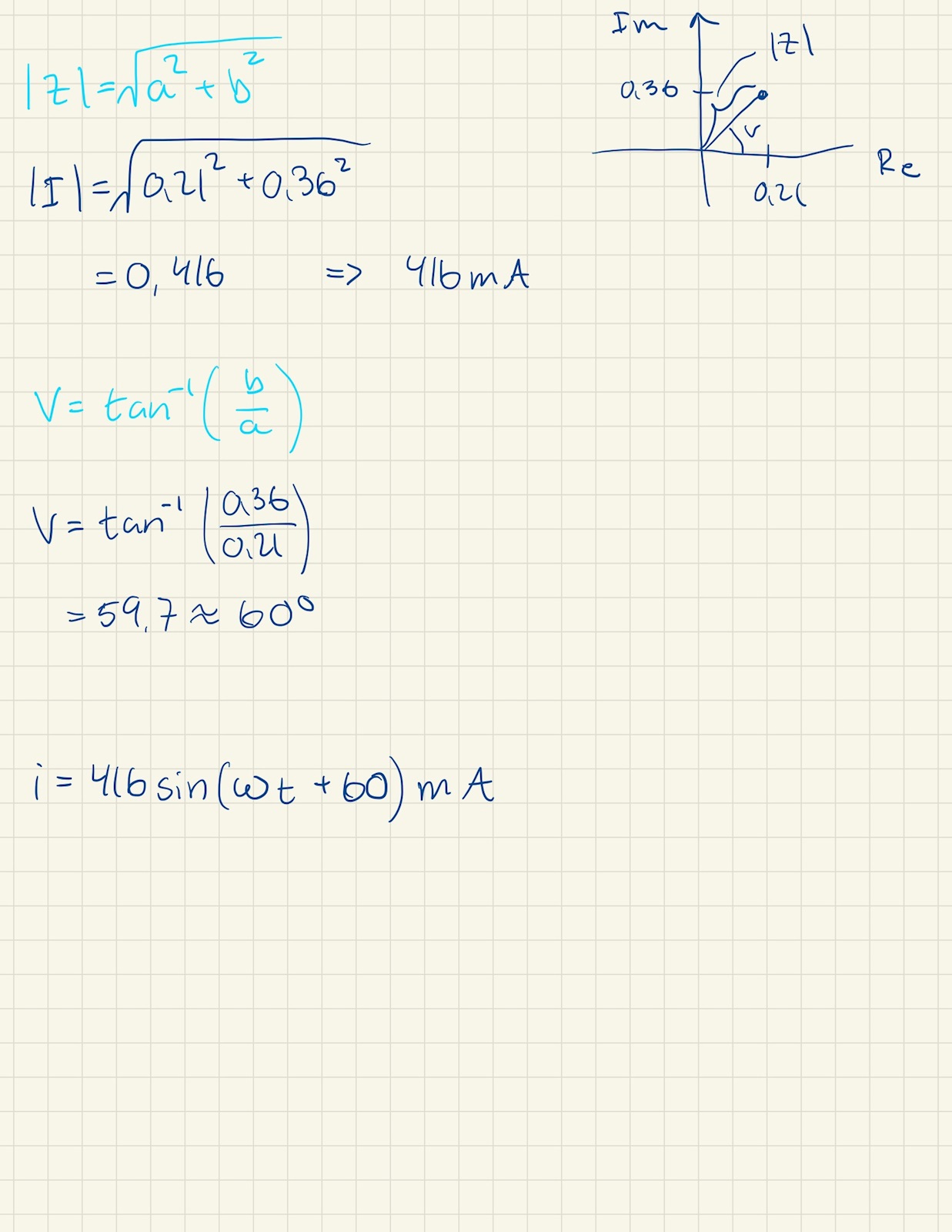
Stort tack!
Däremot så förstår jag inte b-uppg. (eller jag får i alla fall inte samma svar som facit)
Där jag har gjort följande:

416mA är amplituden, dvs toppvärdet.
Om du ska räkna effekten så ska du ha RMS-värdet. För en ren sinus som vi har här är det ju bara att dividera med...
Men de ska bli lika, det är ju bara i resistansen som det utvecklas någon aktiv effekt.
Ah, ska dela med , en annan fråga som dök upp är att i facit anger de olika formler för att beräkna "avgivna effekten" (b-uppg. ) och "förbrukade effekten" (c-upp.g ). Nu visade sig fallet att det gav samma svar men på denna sida i kursboken:

läser jag mig till att "aktiva effekten i en passiv linjär tvåpol" menas då med resistorns förbrukade effekt? Eller kan man använda de två formlerna oberoende på situation?
Förutsatt att nämnaren hade varit rätt i inlägg #1 skulle du kunnat omvandla till exponentiell form redan där och utnyttja potenslagarna :).
För aktiv effekt, som brukar betecknas P, är spänning och ström i fas. Det är fallet med spänning och ström i en resistor. Denna kan uträtta ett arbete som ljus, rörelse eller i resistorn, värme.
När det gäller kapacitansen är spänning och ström 90 grader fasförskjutna. Den kallas reaktiv effekt och brukar betecknas Q.
I en kombination av kapacitans och resistans så får vi en fasförskjutning på 0-90 grader. P och Q bildar det man kallar skenbar effekt som brukar betecknas med S.

fner skrev:Förutsatt att nämnaren hade varit rätt i inlägg #1 skulle du kunnat omvandla till exponentiell form redan där och utnyttja potenslagarna :).
Hummm... Menar du på b-uppgiften nu?
ThomasN skrev:För aktiv effekt, som brukar betecknas P, är spänning och ström i fas. Det är fallet med spänning och ström i en resistor. Denna kan uträtta ett arbete som ljus, rörelse eller i resistorn, värme.
När det gäller kapacitansen är spänning och ström 90 grader fasförskjutna. Den kallas reaktiv effekt och brukar betecknas Q.
I en kombination av kapacitans och resistans så får vi en fasförskjutning på 0-90 grader. P och Q bildar det man kallar skenbar effekt som brukar betecknas med S.
Okej... Men då behöver jag veta någon av S,P eller Q för att använda de sambanden, vilket jag inte är riktigt säker på om vi vet?
Nej jag menar på a)-uppgiften, se nedan. Vet att du har löst den redan men detta är ett alternativt sätt.

Det frågades bara efter uteffekten från generatorn och effektutvecklingen i resistansen så vi behöver inte räkna ut eller veta Q och S. Jag ville bara ge lite mer "kött på benen".
Du har väl redan räknat ut dem, stämde det?
fner skrev:Nej jag menar på a)-uppgiften, se nedan. Vet att du har löst den redan men detta är ett alternativt sätt.
Ah! Okej, tack!
ThomasN skrev:Det frågades bara efter uteffekten från generatorn och effektutvecklingen i resistansen så vi behöver inte räkna ut eller veta Q och S. Jag ville bara ge lite mer "kött på benen".
Du har väl redan räknat ut dem, stämde det?
Tyvärr inte.....
Däremot så förstår jag inte b-uppg. (eller jag får i alla fall inte samma svar som facit)
Där jag har gjort följande:

Dessa är toppvärden på ström och spänning. Om du använder RMS-värden i stället, stämmer det då?
Ah, blandat ihop det i tråden lite, detta har jag gjort:

(vilket ger rätt svar, men facit anger en annan formel). Men som jag nämnde i #10 undrar jag lite om formlerna där kunde blandas, eller om de båda hörde till varsitt fall. Och så som jag tolkar #12 så är de inte samma?
Lite osäker på vad du menar med blandas. Menar du
Men här står ju hur de här de hänger ihop:
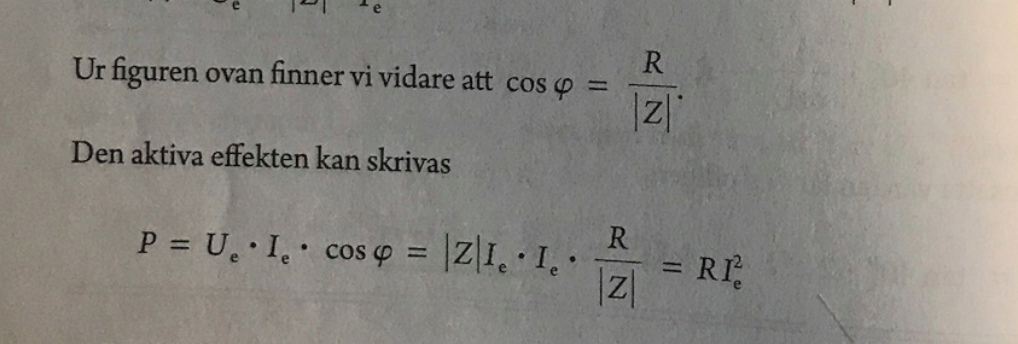
*faceplam* (lite pinsamt) men, tack!