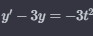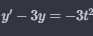Allmänna lösningen till en differentialekvation av första ordningen:)
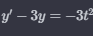
Jag fick fram den homogena lösningen till y=Ce^3t
När jag började på den partikulära kom jag fram till a -3(a*t^2 + b*t+c)=3t^2
Jag forsätter att utveckla det men jag insåg att det förmodligen inte ska stå a framför -3(a*t^2 + b*t+c)=3t^2 utan något annat, jag antog att det var a först då det var så på enklare uppgiften som inte hade något upphöjning men nu är jag lite osäker vad ja ska göra härnäst.
Agnessss12 skrev:
Jag fick fram den homogena lösningen till y=Ce^3t
När jag började på den partikulära kom jag fram till a -3(a*t^2 + b*t+c)=3t^2
Jag forsätter att utveckla det men jag insåg att det förmodligen inte ska stå a framför -3(a*t^2 + b*t+c)=3t^2 utan något annat, jag antog att det var a först då det var så på enklare uppgiften som inte hade något upphöjning men nu är jag lite osäker vad ja ska göra härnäst.
Menar du att du ansatte y = at2+bt+c? Vad blev derivatan y'?
Smaragdalena skrev:Agnessss12 skrev:
Jag fick fram den homogena lösningen till y=Ce^3t
När jag började på den partikulära kom jag fram till a -3(a*t^2 + b*t+c)=3t^2
Jag forsätter att utveckla det men jag insåg att det förmodligen inte ska stå a framför -3(a*t^2 + b*t+c)=3t^2 utan något annat, jag antog att det var a först då det var så på enklare uppgiften som inte hade något upphöjning men nu är jag lite osäker vad ja ska göra härnäst.
Menar du att du ansatte y = at2+bt+c? Vad blev derivatan y'?
Nu hänger ja inte riktigt med, men ja jag antog att y=at2+bt+c pågrund av att hela ekvationen var = -3t^2. Har jag gjort fel? eller vad är nästa steg?
Har funderat lite om jag deriverar blir inte det 2at+b? eller blir det kanske 2at-b? lite osäker men jag antar att det är positivt.
låter -3at^2 + 2at -3bt +b-3c=3t^2 korrekt? Jag tycker det bör stämma men jag är förmodligen ute och cyklar lite.
Du har y'-3y = -3t2. Om y = at2+bt+c så blir y' = 2at+b. Sätter vi in y och y' får vi
2at+b-3(at2+bt+c) = -3t2. Då blir det -3at2 + (2a-3b)t -3c = 3t2. För att detta skall stämma för alla vörden på t krävs det att -3a = 3, 2a-3b = 0 och -3c = 0. Kommer du vidare?
Smaragdalena skrev:Du har y'-3y = -3t2. Om y = at2+bt+c så blir y' = 2at+b. Sätter vi in y och y' får vi
2at+b-3(at2+bt+c) = -3t2. Då blir det -3at2 + (2a-3b)t -3c = 3t2. För att detta skall stämma för alla vörden på t krävs det att -3a = 3, 2a-3b = 0 och -3c = 0. Kommer du vidare?
jaaa halvt, jag fick a till 1 b till -2/3 och c till -2/9 men i facit står det att a = t^2 b till 2t/3 och c till 2/9