Algebran fundamentalsats
Jag hade lite frågor kring komplexa tal och algebrans fundamental sats.
- Vad är skillnaden mellan en polynom och en ekvation? Boken flip-floppar fram och tillbaka med dessa termer och jag blir lite förvirrad när de använder dem. Finns det någon skillnad, eller är det bara en ekvation när det är =0?
- Vad är skillnaden mellan en polynom eller ekvations nollställen och rötter? Är nollställer och rötter samma sak?
- För nedre ekvation, finns det 4 rötter enligt algebrans fundamentalsats. Men de behöver inte vara reella tal, de kan också vara komplexa.

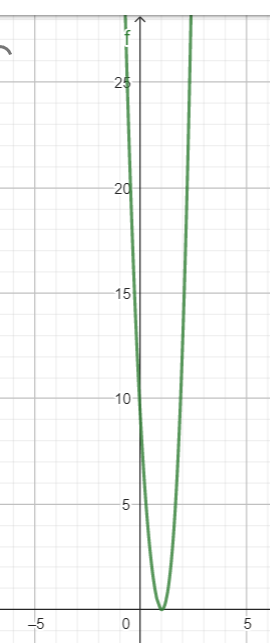

När man löser ut ekvationen får man x1=3i, x2=-3i, x3=1, och x4=1, alltså en dubbelrot vid x=1. Detta betyder att på grafen ser man bara dubbelroten vid x=1 och inte komplexa rötterna eftersom de är imaginära och kan bara ses på komplexatalplanet. Har jag uppfattat detta rätt?
Förlåt för mishmash av frågor här men vill bara se till att jag förstår allt. Tack!
Ett polynom är ett uttryck, sätter du in ett värde på x så får du ut ett tal
En ekvation är ett påstående A = B. För vissa x är A lika med B, det gäller att hitta dessa
x.
Men polynomet x2+x+7 är inget påstående.
Ett polynom har nollställen. En ekvation har rötter
ETT polynom är en typ av funktion. Den kan ha Nollställen (=ställen där den är = 0) Polynom har inte rötter.
En ekvation är ett påstående (utsaga). Den kan vara sann eller falsk. Att lösa en ekvation är att ta reda på de värden som gör utsagan sann. Dessa värden kallas rötter.
Resonemanget kring din figur är OK.
De komplexa (dvs icke-reella) rötterna syns inte i ett ”vanligt” koordinatsystem.
Det är väldigt svårt att göra en grafisk beskrivning av ett komplext samband för både definitionsmängd och värdemängd är tvådimensionella. Redan tre dimensioner kräver konstnärlig talang att rita på ett tvådimensionellt papper, med fyra dimensioner att hantera får man hitta andra sätt.


