Algebra, problemlösning ekvation
På en tipspromenad fanns 20 frågor. för varje rätt fick man 5 poäng men för varje fel blev det 2 minuspoäng. Jonas svarade på alla frågor och fick 58 poäng. På hur många frågor svarade han rätt?
Förstår inte riktigt men har kommit så långt: 5x-2y=58 och jag vet att jag måste byta ut y med något annat så att man kan beräkna ekvationen men vet ej vad jag ska byta ut y med.
Hej.
Bra början!
Jag antar att x är antalet rätta svar och att y är antalet felaktiga svar.
Du undrar nu vad du kan byta ut y mot flr att kunna lösa ekvationen.
Tips: Det var 20 frågor totalt.
men förstår fortfarande inte...hur tänker jag
Svarar man x antal rätt på 20 frågor, hur många frågor har man då svarat fel på uttryckt i x?
pluggnörd skrev:men förstår fortfarande inte...hur tänker jag
Du kan tänka att x+y = 20.
sictransit skrev:Svarar man x antal rätt på 20 frågor, hur många frågor har man då svarat fel på uttryckt i x?
20-x?
Just det. Sätt in detta värde på y i ekvationen 5x-2y=58. Kommer du vidare?
Smaragdalena skrev:Just det. Sätt in detta värde på y i ekvationen 5x-2y=58. Kommer du vidare?
så jag byter ut Y med 20-x?
då blir det såhär 5x-2(20-x)?
pluggnörd skrev:Smaragdalena skrev:Just det. Sätt in detta värde på y i ekvationen 5x-2y=58. Kommer du vidare?
så jag byter ut Y med 20-x?
då blir det såhär 5x-2(20-x)?
Ja, men tappa inte poängsumman för annars får du ingen ekvation att lösa.
sictransit skrev:pluggnörd skrev:Smaragdalena skrev:Just det. Sätt in detta värde på y i ekvationen 5x-2y=58. Kommer du vidare?
så jag byter ut Y med 20-x?
då blir det såhär 5x-2(20-x)?Ja, men tappa inte poängsumman för annars får du ingen ekvation att lösa.
Jaha oj jag menade 5x-2(20-x)=58
Ja, det stämmer.
Yngve skrev:Ja, det stämmer.
tack för hjälpen
men om det är inget besvär skulle du kunna ge mig en liknande uppgift som jag ska lösa själv för att jag vill vara säker på att jag kan lösa sådana uppgifter på kommande matteprov, tack!
Ja, men först ska jag tipsa om en alternativ lösning på problemet:
Gissning plus smart justering av gissning:
Gissa först att Jonas hade alla rätt, dvs 20 rätt.
Då skulle han haft 20*5 = 100 poäng.
Alltså måste han ha haft fel på ett antal frågor.
Vi tar nu reda på hur många av svaren som var fel.
För varje felaktigt svar får vi dra bort 5+2 = 7 poäng från vår ursprungsgissning (minus 5 poäng eftersom svaret inte var rätt och minus ytterligare 2 poäng som "straff" för felaktigt svar).
Vi vet att Jonas hade 58 poäng, vilket betyder att vi ska dra bort 100-58 = 42 poäng från vår ursprungsgissning.
42 poäng motsvarar 42/7 = 6 frågor.
Alltså hade Jonas fel på 6 frågor.
Alltså hade Jonas rätt på 20-6 = 14 frågor.
Ytterligare en metod:
Upprepade gissningar enligt "intervallhalveringsmetoden":
- Gissa först ungefär i mitten av intervallet 0- 20 rätt, dvs att Jonas svarade rätt på 10 av frågorna. Då skulle han haft 10 rätt och 10 fel, vilket skulle ha givit honom 10*5-10*2 = 30 poäng. Det är för lite. Han måste haft fler rätt, dvs i intervallet 11-20 rätt.
- Gissa nu ungefär i mitten av intervallet 11-20 rätt, dvs att Jonas svarade rätt på 15 frågor. Då skulle han haft 15 rätt och 5 fel, vilket skulle ha givit honom 15*5-5*2 = 65 poäng. Det är för mycket. Han måste haft färre rätt, dvs i intervallet 11-14 rätt.
- Gissa nu ungefär i mitten av intervallet 11-14 rätt, dvs att Jonas svarade rätt på 12 frågor. Då skulle han haft 12 rätt och 8 fel, vilket skulle ha givit honom 12*5-8*2 = 44 poäng. Det är för lite. Han måste haft fler rätt, dvs i intervallet 13-14 rätt.
- Gissa nu ungefär i mitten av intervallet 13-14 rätt, dvs att Jonas svarade rätt på 14 frågor. Då skulle han haft 14 rätt och 6 fel, vilket skulle ha givit honom 14*5-6*2 = 58 poäng. Det stämmer!
Alltså hade Jonas 14 rätt.
Denna metod är generellt sett väldigt snabb och har den fördelen att den är hyfsat intuitiv.
Exempeluppgift:
Bonden Sara har givit sin matteintresserade dotter Ella följande mattekluring:
"På vår bondgård har vi kor och höns. Tillsammans har de 20 huvuden och 56 ben. Hur många kor och hur många höns har vi?"
Ella kämpar ett tag med uppgiften men kör fast.
========
Din uppgift är nu att förklara för Ella hur hon kan bära sig åt för att lösa kluringen.
Förutom Yngves utmärkta iterativa metoder vill jag även lyfta möjligheten att lösa grafiskt.
Ibland är det ett snabbt sätt att åtminstone se var lösningen borde hamna.
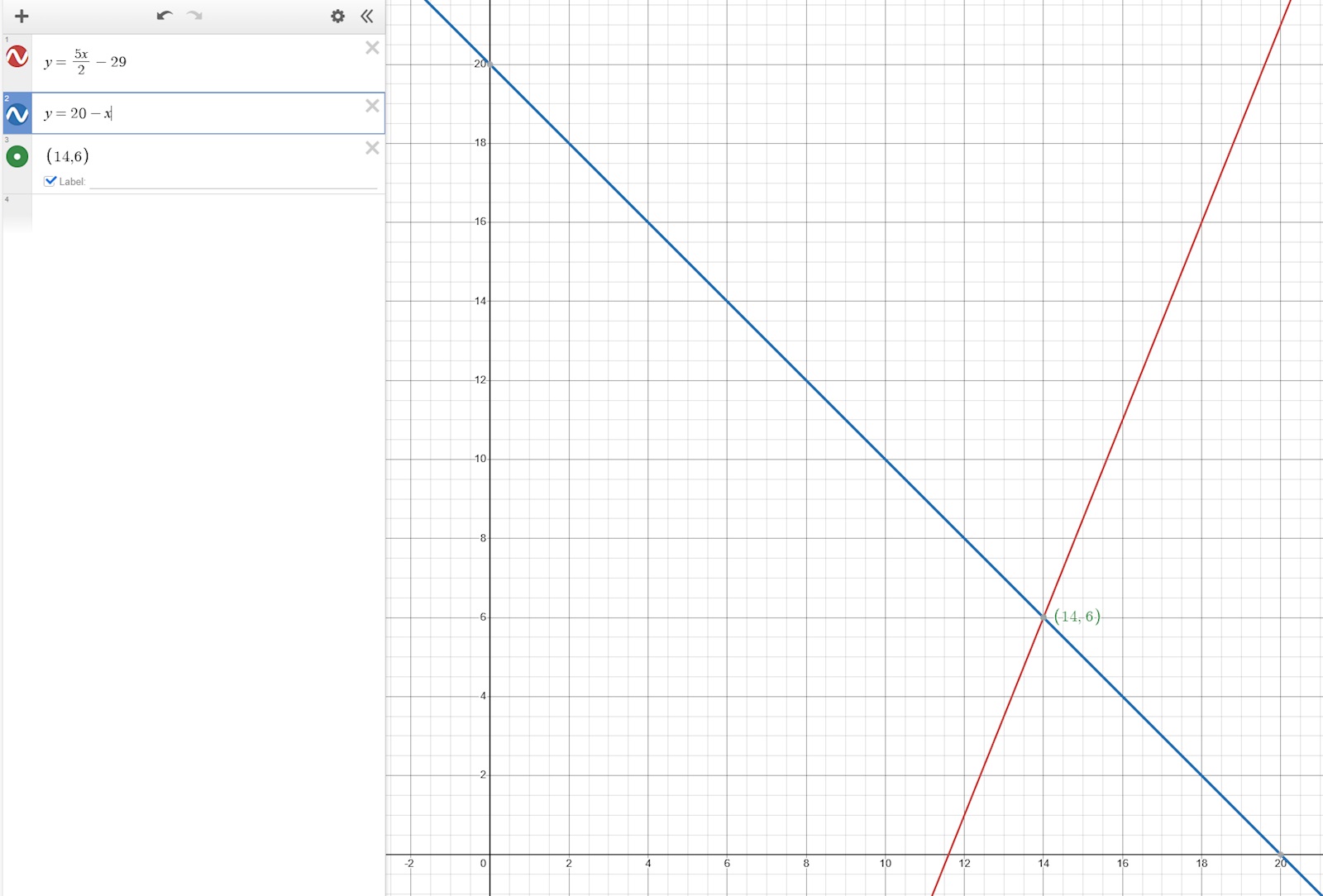
Vi skriver om din ekvation 5x-2y=58 och får en linje vi kan rita ut: . Det räcker med att räkna ut två punkter och ta fram linjalen.
Vi har även linjen y=20-x.
Yngve skrev:Ja, men först ska jag tipsa om en alternativ lösning på problemet:
Gissning plus smart justering av gissning:
Gissa först att Jonas hade alla rätt, dvs 20 rätt.
Då skulle han haft 20*5 = 100 poäng.
Alltså måste han ha haft fel på ett antal frågor.
Vi tar nu reda på hur många av svaren som var fel.
För varje felaktigt svar får vi dra bort 5+2 = 7 poäng från vår ursprungsgissning (minus 5 poäng eftersom svaret inte var rätt och minus ytterligare 2 poäng som "straff" för felaktigt svar).
Vi vet att Jonas hade 58 poäng, vilket betyder att vi ska dra bort 100-58 = 42 poäng från vår ursprungsgissning.
42 poäng motsvarar 42/7 = 6 frågor.
Alltså hade Jonas fel på 6 frågor.
Alltså hade Jonas rätt på 20-6 = 14 frågor.
Tack för metoderna! men här i denna metoden varför måste jag räkna ut antal missade poäng (42) och dividera på 7, kan man inte bara ta antal poäng han fick och dividera med 7?
Nej, 7 ör poängskillnaden mellan ett korrekt svar (+5 poäng) och ett felaktigt svar (-2 poäng).
Så att rökna med 7 poäng är endast relevant när vi pratar om att byta ut ett korrekt svar mot ett felaktigt (ger -7 poäng) eller tvärtom, att byta ut ett felaktigt svar mot ett korrekt svar (ger +7 poäng).
Att dividera 58 poäng med 7 har inget med uppgiften att göra, eftersom 58 ges av en blandning av korrekta och felaktiga svar.
Yngve skrev:Nej, 7 ör poängskillnaden mellan ett korrekt svar (+5 poäng) och ett felaktigt svar (-2 poäng).
Så att rökna med 7 poäng är endast relevant när vi pratar om att byta ut ett korrekt svar mot ett felaktigt (ger -7 poäng) eller tvärtom, att byta ut ett felaktigt svar mot ett korrekt svar (ger +7 poäng).
Att dividera 58 poäng med 7 har inget med uppgiften att göra, eftersom 58 ges av en blandning av korrekta och felaktiga svar.
Jaha nu förstår jag 58 är en blandning av korrekta och fel svar medan 42 är bara fel svar(missade poäng+minuspoäng)
Ja 42 är, utöver att vara svaret på livet, universum och allting 😉, även poängskillnaden mellan "alla rätt" och Jonas faktiska resultat.
Varje felaktigt svar minskar totalpoängen med 7.
Yngve skrev:Ja 42 är, utöver att vara svaret på livet, universum och allting 😉, även poängskillnaden mellan "alla rätt" och Jonas faktiska resultat.
Varje felaktigt svar minskar totalpoängen med 7.
vad menar du med "poängskillnaden mellan alla rätt och jonas faktiska resultat"?
Om Jonas hade haft rätt på alla 20 frågorna skulle han ha haft 20.5 = 100 poäng. Nu hade Jonas 58 poäng, så skillnaden mellan "alla rätt" och Jonas' resultat är 100-58 = 42 poäng.
Yngve skrev:Exempeluppgift:
Bonden Sara har givit sin matteintresserade dotter Ella följande mattekluring:
"På vår bondgård har vi kor och höns. Tillsammans har de 20 huvuden och 56 ben. Hur många kor och hur många höns har vi?"
Ella kämpar ett tag med uppgiften men kör fast.
========
Din uppgift är nu att förklara för Ella hur hon kan bära sig åt för att lösa kluringen.
y=höns x=ko
jag började med 4x+2y=56
sen x+y=20 då är y=20-x
sen byter jag ut y mot (20-x)
då blir det: 4x+2(20-x)=56
4x+40-2x=56
2x+40=56
2x+40-40=56-40
2x=16
x=8
8 kor och 24 höns
har jag rätt?
Du kan och bör alltid kontrollera ditt svar.
Om det är 8 kor och 24 höns,
- hur många huvuden finns det då?
- hur många ben finns det då?
Stämmer det med utsprungsuppgifterna?
I så fall är svaret rätt, annars inte.
Yngve skrev:Du kan och bör alltid kontrollera ditt svar.
Om det är 8 kor och 24 höns,
- hur många huvuden finns det då?
- hur många ben finns det då?
Stämmer det med utsprungsuppgifterna?
I så fall är svaret rätt, annars inte.
va, men vad för fel har jag gjort!? kan du ge mig någon ledtråd?
Allt ser jättebra ut och det är helt rätt.
Ända fram till sista raden.
Yngve skrev:Allt ser jättebra ut och det är helt rätt.
Ända fram till sista raden.
vad menar du? jag försökte att kolla hur många ben det fanns tillsammans och 8 kor+24 höns= 8*4+24*2= 80 ben, men det är ju 56 ben hur kan det vara rätt!?
Näst sista raden i svar #23 stämmer, nämligen att x = 8.
Hur tänkte du efter det?
Yngve skrev:Näst sista raden i svar #23 stämmer, nämligen att x = 8.
Hur tänkte du efter det?
jag tänkte att x stod för antalet kor
Ja, bra. Det är alltså 8 kor.
Men hur kom du fram till att det är 24 hönor?
Yngve skrev:Ja, bra. Det är alltså 8 kor.
Men hur kom du fram till att det är 24 hönor?
x=8
2(20-x)
40-16=24
pluggnörd skrev:Yngve skrev:Ja, bra. Det är alltså 8 kor.
Men hur kom du fram till att det är 24 hönor?
x=8
2(20-x)
40-16=24
OK, men termen 2(20-x) står för antalet ben som hönorna har sammanlagt, inte antalet hönor.
Antalet hönor är ju y, som du mycket riktigt skrev i början av din lösning.
Yngve skrev:pluggnörd skrev:Yngve skrev:Ja, bra. Det är alltså 8 kor.
Men hur kom du fram till att det är 24 hönor?
x=8
2(20-x)
40-16=24
OK, men termen 2(20-x) står för antalet ben som hönorna har sammanlagt, inte antalet hönor.
Antalet hönor är ju y, som du mycket riktigt skrev i början av din lösning.
Jahaaaa förstod fel, då är det 20-8=12
svar: 12 hönor och 8 kor
Har du kontrollerat ditt nya svar enligt metoden i svar #24?
Yngve skrev:Har du kontrollerat ditt nya svar enligt metoden i svar #24?
japp, och det ser rätt ut ! tack så mycket för hjälpen :) nu är jag mer självsäker
Bra gjort!



