Absolutbelopp med två lösningar

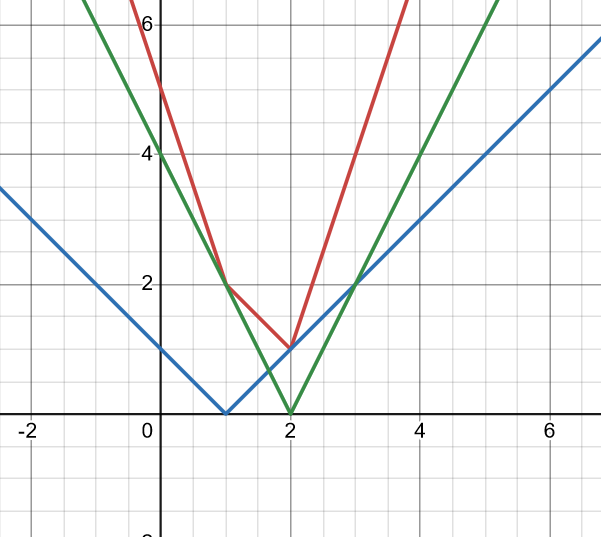
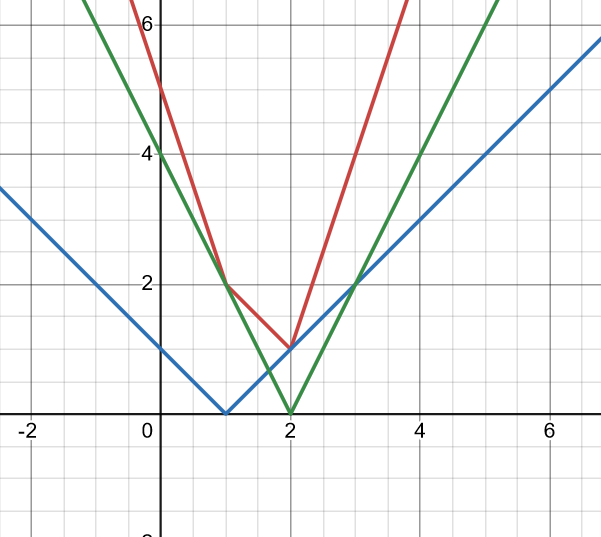
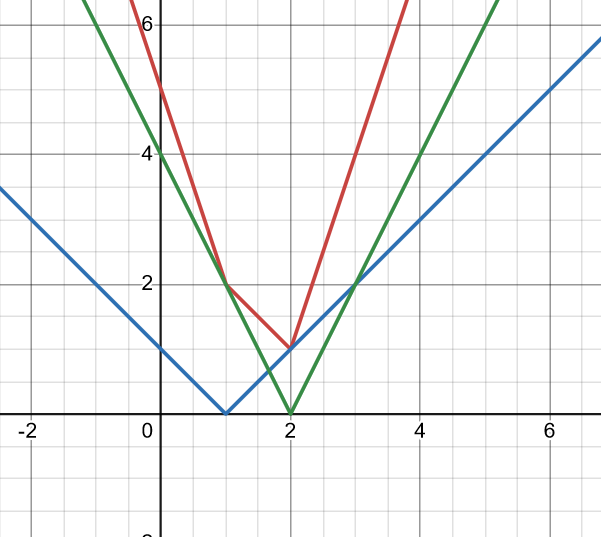
Som vanligt är det enklast att rita.

EDIT: Det är den röda linjen som gäller, de andra är |x-1| respektive -2|x-2|. Jag ritade inte in någon linje a = y, du kan nog ändå se vilka värden på a som ger två skärningar med den röda kurvan.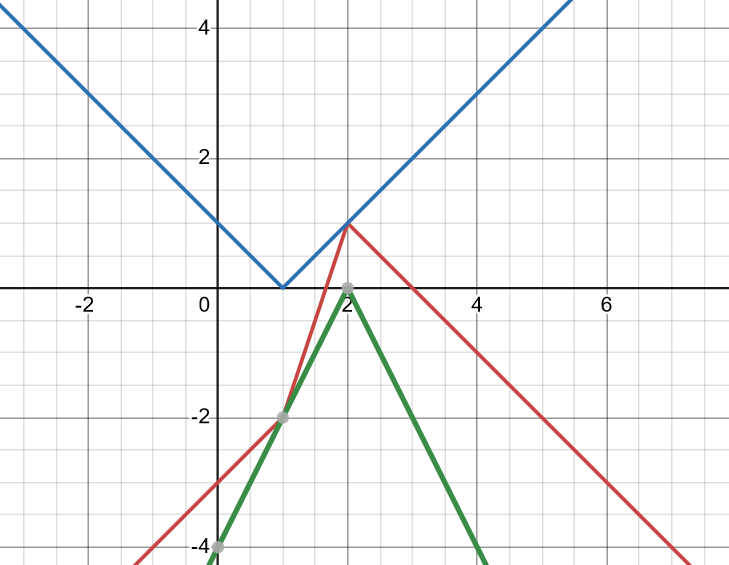

Axiom skrev:

[...]

1) $$\begin{gathered} x\ge 1 \\ x⩾2 --> x⩾2 \end{gathered}$$

[...]

2) $$\begin{gathered} x<1 \\ x<2 --> x<1 \end{gathered}$$

För de två andra fallen blir ekvationen ogiltig.

[...]

Vilka två andra fall?

Det finns bara följande tre fall:

• $x<1$
• $1\leq x<2$
• $x\geq2$

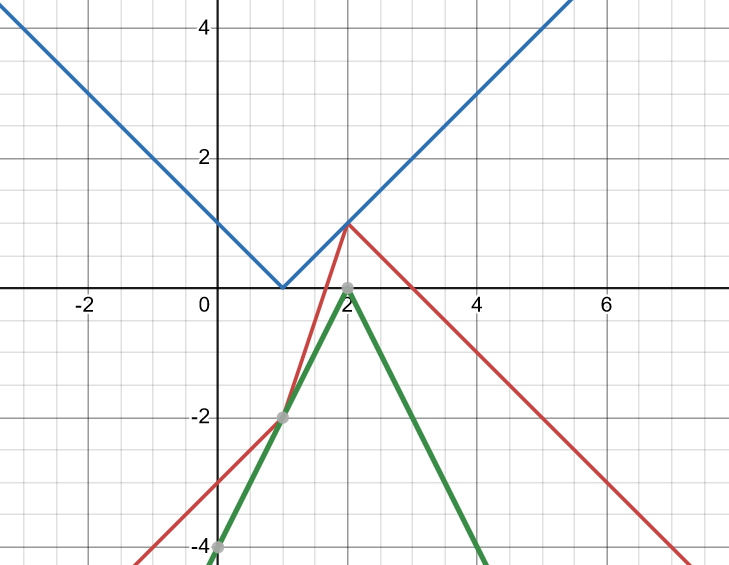
Det hade blivit lite fel i min graf. Förhoppningsvis är den rätt nu:

Yngve skrev:

Axiom skrev:

[...]

1) $$\begin{gathered} x\ge 1 \\ x⩾2 --> x⩾2 \end{gathered}$$

[...]

2) $$\begin{gathered} x<1 \\ x<2 --> x<1 \end{gathered}$$

För de två andra fallen blir ekvationen ogiltig.

[...]

Vilka två andra fall?

Det finns bara följande tre fall:

• $x<1$
• $1\leq x<2$
• $x\geq2$

Ena absolutbeloppet hade kunnat vara positivt och de andra negativt eller tvärtom

Yngve skrev:

Axiom skrev:

[...]

1) $$\begin{gathered} x\ge 1 \\ x⩾2 --> x⩾2 \end{gathered}$$

[...]

2) $$\begin{gathered} x<1 \\ x<2 --> x<1 \end{gathered}$$

För de två andra fallen blir ekvationen ogiltig.

[...]

Vilka två andra fall?

Det finns bara följande tre fall:

• $x<1$
• $1\leq x<2$
• $x\geq2$

Men hur får man att a>1

Axiom skrev:
Men hur får man att a>1

Titta på bilden. Ser du att om en linje y = a har en skärningspunkt med den röda kurvan om a = 1, två skärningspunkter om a > 1 och ingen skärningspunkt om a < 1?

Smaragdalena skrev:

...

Axiom skrev:

Men hur får man att a>1

Du kan antingen lösa uppgiften grafiskt som Smaragdalena visade eller algebraiskt som du själv började på.

Dela då upp uppgiften i de tre ovan angivna fallen, skriv om uttrycken utan absolutbelopp och lös ekvationen i respektive intervall.

Förkasta alla lösningar som inte ligger I respektive intervall.

Yngve skrev:

Axiom skrev:

Men hur får man att a>1

Du kan antingen lösa uppgiften grafiskt som Smaragdalena visade eller algebraiskt som du själv började på.

Dela då upp uppgiften i de tre ovan angivna fallen, skriv om uttrycken utan absolutbelopp och lös ekvationen i respektive intervall.

Förkasta alla lösningar som inte ligger I respektive intervall.

Även om grafiska lösningar är väldigt fina och intuitiva så tror jag tyvärr att det förväntas att man ska göra en algebraisk lösning. Men när jag försöker lösa den algebraiskt som ovan får jag ju fel svar, vad har jag gjort för fel?

Smaragdalena skrev:

Som vanligt är det enklast att rita.

EDIT: Det är den röda linjen som gäller, de andra är |x-1| respektive -2|x-2|. Jag ritade inte in någon linje a = y, du kan nog ändå se vilka värden på a som ger två skärningar med den röda kurvan.

Jag tor det, är det den blåa linjen som representerar a?

Den blå linjen är y = |x-1|. Linjen y = a är en vågrät linje.

Smaragdalena skrev:

Det hade blivit lite fel i min graf. Förhoppningsvis är den rätt nu:

Vi söker efter vilka y värden (a) som det kommer finnas två x-värden, så borde det inte vara för alla a>1 och a<1 För att vid a=1 så finns det bara ett x-värde

Hur många skärningspunkter finns det mellan den röda linjen och linjen y = a om a < 1?

Axiom skrev:

Vi söker efter vilka y värden (a) som det kommer finnas två x-värden, så borde det inte vara för alla a>1 och a<1 För att vid a=1 så finns det bara ett x-värde

Nej inte riktigt.

Jag har här ritat graferna

• y = |x-1|+2|x-2|
• y = 0,5
• y = 1
• y = 1,5

Hjälper det dig att hitta svaret?

Yngve skrev:

Axiom skrev:

Vi söker efter vilka y värden (a) som det kommer finnas två x-värden, så borde det inte vara för alla a>1 och a<1 För att vid a=1 så finns det bara ett x-värde

Nej inte riktigt.

Jag har här ritat graferna

• y = |x-1|+2|x-2|
• y = 0,5
• y = 1
• y = 1,5

Hjälper det dig att hitta svaret?

Jo för alla a>1 finns det två svar, men hur skulle man lösa detta algebraiskt ?

Vi har ekvationen |x-1|+2|x-2| = a. Funktionen består av tre olika räta linjer med brytpunkter vid x = 1 och x = 2.

Om x < 1 så är vänsterledet |x-1|+2|x-2| = 1-x+2(2-x) = -3x+5. [1]
Om 1 < x < 2 så är vänsterledet |x-1|+2|x-2| = x-1+2(2-x) = -x+3. [2]
Om x > 2 så är vänsterledet |x-1|+2|x-2| = x-1+2(x-2) = 3x-5. [3]

Linjen [1] har sitt minsta värde y = 2 för x = 1.
Linjen [2] har sitt största värde y = 2 för x = 1 och sitt minsta värde y = 1 för x = 2.
Linjen [3] har sitt minsta värde y = 1 för x = 2.

Vänsterledet har alltså sitt minsta värde 1, och antar alla värden som är större än så. Alltså gäller det att ekvationen har två rötter för alla a > 1.

Man kan skriva att "Linjen [1] är en rät linje med negativ riktningskoefficient, så den antar sitt största värde längst till höger i sitt intervall" och motsvarande för de andra linjerna om man tycker det behövs.

Smaragdalena skrev:

Vi har ekvationen |x-1|+2|x-2| = a. Funktionen består av tre olika räta linjer med brytpunkter vid x = 1 och x = 2.

Om x < 1 så är vänsterledet |x-1|+2|x-2| = 1-x+2(2-x) = -3x+5. [1]
Om 1 < x < 2 så är vänsterledet |x-1|+2|x-2| = x-1+2(2-x) = -x+3. [2]
Om x > 2 så är vänsterledet |x-1|+2|x-2| = x-1+2(x-2) = 3x-5. [3]

Linjen [1] har sitt minsta värde y = 2 för x = 1.
Linjen [2] har sitt största värde y = 2 för x = 1 och sitt minsta värde y = 1 för x = 2.
Linjen [3] har sitt minsta värde y = 1 för x = 2.

Vänsterledet har alltså sitt minsta värde 1, och antar alla värden som är större än så. Alltså gäller det att ekvationen har två rötter för alla a > 1.

Man kan skriva att "Linjen [1] är en rät linje med negativ riktningskoefficient, så den antar sitt största värde längst till höger i sitt intervall" och motsvarande för de andra linjerna om man tycker det behövs.

Hur fick du reda på de minsta värdena?

Jag satte in x-värdena i de aktuella linjära funktionerna, precis som jag lärde mig redan på högstadiet.

Smaragdalena skrev:

Jag satte in x-värdena i de aktuella linjära funktionerna, precis som jag lärde mig redan på högstadiet.

Att använda funktionerna för att plugga in värdena var inte den metod som jag uppfattade att man skulle använda på sådana här uppgifter utan att se för vilka värden a och b existerar på tallinjen och på så sätt se ett intervall mellan dem

Varifrån "uppfattade" du detta? Finns det kontext som du inte har givit oss?

Smaragdalena skrev:

Varifrån "uppfattade" du detta? Finns det kontext som du inte har givit oss?

Då hänvisar jag dig till indelningen av denna uppgift där det står att detta är Matematik/Universitet och eftersom jag går på föreläsningar har jag en aning om vilka regler som gäller för den här typen av uppgifter. T.ex. vet jag att sedan när det är dags för tentamen går det inte att lösa den här typen av uppgifter geometriskt. (Och när det gäller t.ex. mängder gäller inte venndiagram som ett bevis. Eftersom venndiagram bara en visualisering och inte ett bevis inom matematiken. Denna kontext uppfattade jag som självklar men jag har skrivit det i alla andra av mina inlägg på Universitetsnivå när det har funnits sådana förhållanden. Annars är allt jag angivit allt material jag haft tillgång till. 

Det gäller lite andra tillvägagångssätt på universitetsnivå. Vilket också är synd för att t.ex. venndiagram är väldigt trevliga tycker jag :)

Inte kan väl ditt universitet vara så korkat att de tackar nej till de matematiskt korrekta hjälpmedel som finns? Självklart är inte endast ett Venn-diagram ett bevis, men det är ett utmärkt hjälpmedel för att komma fram till vad det är man skall bevisa.

Smaragdalena skrev:

Inte kan väl ditt universitet vara så korkat att de tackar nej till de matematiskt korrekta hjälpmedel som finns? Självklart är inte endast ett Venn-diagram ett bevis, men det är ett utmärkt hjälpmedel för att komma fram till vad det är man skall bevisa.

Som jag sa det är inte ett bevis utan en sorts visualiserings verktyg och de flesta uppgifterna med mängder inom universitet handlar om just bevis därav får man inga poäng om man använder venndiagram som ett bevis eller ens för det anologierna om + och * men nu svävar du ut lite mycket från uppgiften tycker jag. Att direkt anklaga mitt universitet för att vara "korkat" har ingenting med uppgiften att göra. Du behöver inte hjälpa mig men lägg inte onödiga kommentarer som inte tillhör ämnet tack.

Förslag på algebraisk lösning:

Dela in definitionsmängden i de tre intervallen I₁, I₂ och I₃ enligt svar #3.

Ekvationen får då följande utseende i de tre intervallen.

I₁ ($x<1$):

(1-x)+2(2-x) = a, dvs 5-3x = a. Ekvationen har en enda lösning i detta intervall om a > 2.

I₂ ($1\leq x<2$):

(x-1)+2(2-x) = a, dvs 3-x = a. Ekvationen har en enda lösning i detta intervall om a > 1.

I₃ ($x\geq 2$):

(x-1)+2(x-2) = a, dvs 3x-5 = a. Ekvationen har en enda lösning i detta intervall om a $\geq$ 1.

=====

För att ursprungsekvationen ska ha två lösningar måste samma a-värde ge en lösning i två av de tre intervallen.

Enligt ovanstående ser vi att

• Om a < 1 så saknas lösning i alla intervall.
• Om a = 1 så finns en enda lösning i intervallet   I₃
• Om 1 < a < 2 så finns en lösning I I₂ och en lösning i I₃
• Om a $\geq$ 2 så finns en lösning I I₁ och en lösning i I₃.

Alltså har ekvationen två lösningar endast då a > 1.

Yngve skrev:

Förslag på algebraisk lösning:

Dela in definitionsmängden i de tre intervallen I₁, I₂ och I₃ enligt svar #3.

Ekvationen får då följande utseende i de tre intervallen.

I₁ ($x<1$):

(1-x)+2(2-x) = a, dvs 5-3x = a. Ekvationen har en enda lösning i detta intervall om a > 2.

I₂ ($1\leq x<2$):

(x-1)+2(2-x) = a, dvs 3-x = a. Ekvationen har en enda lösning i detta intervall om a > 1.

I₃ ($x\geq 2$):

(x-1)+2(x-2) = a, dvs 3x-5 = a. Ekvationen har en enda lösning i detta intervall om a $\geq$ 1.

=====

För att ursprungsekvationen ska ha två lösningar måste samma a-värde ge en lösning i två av de tre intervallen.

Enligt ovanstående ser vi att

• Om a < 1 så saknas lösning i alla intervall.
• Om a = 1 så finns en enda lösning i intervallet   I₃
• Om 1 < a < 2 så finns en lösning I I₂ och en lösning i I₃
• Om a $\geq$ 2 så finns en lösning I I₁ och en lösning i I₃.

Alltså har ekvationen två lösningar endast då a > 1.

Ja i l1 är det att båda i negativa, i l2  att ena absolutbeloppet är positivt andra negativt och i l3 är båda positiva.

Men om om a$\ge$2 ger lösning i l1 och l3 och 1<a<2 ger lösning i l2 och l3 borde inte båda de kunna användas för att få två lösningar?

Läs vad Yngve skriver:

Alltså har ekvationen två lösningar endast då a > 1.

Det innebär alla de intervall du paratar om.

Smaragdalena skrev:

Läs vad Yngve skriver:

Alltså har ekvationen två lösningar endast då a > 1.

Det innebär alla de intervall du paratar om.

a>1 gäller ju inte för alla a>1 om det är så att i l3 behöver 1<a<2 eftersom a<2 behövs för att ge två lösningar i l3? 

Borde inte då svaret vara 1<a<2 eftersom 1<a<2 är en delmängd av a>1?

Jag förstår inte helt

Titta på bilden:

Som vanligt säger den mer än tusen ord. Om 1<a<2 är det l₂ och 1₃ som y = a korsar, om a > 2 är det l₁ och l₃.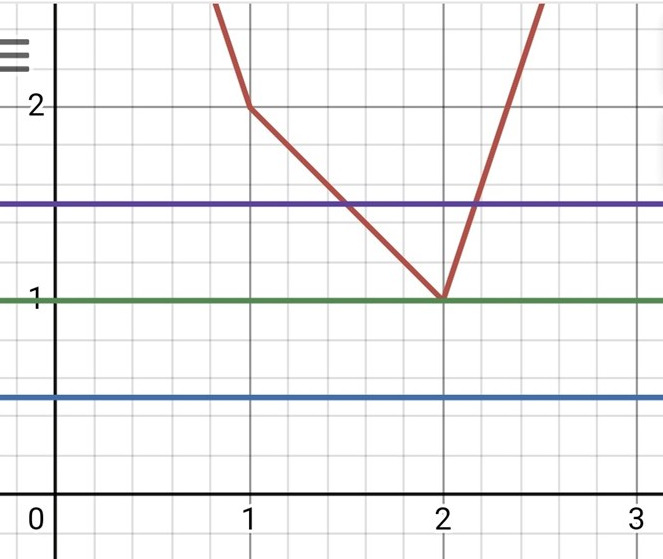

Axiom skrev:

[...]

Men om om a$\ge$2 ger lösning i l1 och l3 och 1<a<2 ger lösning i l2 och l3 borde inte båda de kunna användas för att få två lösningar?

Jag förstår inte riktigt din fråga, kan du försöka förtydliga den?

Axiom skrev:

a>1 gäller ju inte för alla a>1 om det är så att i l3 behöver 1<a<2 eftersom a<2 behövs för att ge två lösningar i l3? 

Borde inte då svaret vara 1<a<2 eftersom 1<a<2 är en delmängd av a>1?

Jag förstår inte helt

Jag förstår inte riktigt dina frågor.

Är du med på följande påståenden?

1. om a < 1 så saknas lösningar i alla 3 intervallen.
2. om a = 1 så saknas lösning i I₁ och I₂, men det finns en lösning i I₃.
3. om 1 < a $\leq$ 2 så saknas lösning i I₁, men der finns en lösning i I₂ och en lösning i I₃.
4. om a > 2 så saknas lösning i I₂, men det finns 1 lösning i I₁ och 1 lösning i I₃.

Smaragdalena skrev:

Jag satte in x-värdena i de aktuella linjära funktionerna, precis som jag lärde mig redan på högstadiet.

Att uttrycka sig på detta nedlåtande sätt är ett brott mot regel 2.1 på Pluggakuten:

"För allas trevnadIakttag vanlig etikett - använd ett vårdat språk, var trevlig och håll god ton."

Skärpning! 

Kommentarer som att ett universitet skulle bete sig "korkat" är onödiga, och bör undvikas, även om de inte formellt sett är regelbrott. /moderator