Absolutbelopp ekvation
Hur skulle ni strukturera upp och lösa denna?
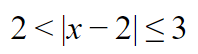
Rita.
Varifrån kommer uppgiften? Absolutbelopp borde inte vara med på högskoleprovet, där det skall räcka med Ma1.
Om du istället vill lösa den algebraiskt så kan du dela upp olikheten i följande två delar:
Område 1: , dvs .
Här gäller att och olikheten blir då .
Område 2: , dvs .
Hör gäller att och olikheten blir då
Kommer du vidare med att lösa dessa olikheter?
Vet inte riktigt om jag förstår, men som jag ser det. Löser jag vardera olikhet för sig och sen ritar ut var de ligger på en tallinje och om de ska vara mer eller mindre än det jag räknade ut, så får jag två intervall där och på så vis får jag svaret.
T.ex. första 2<x-2 => 4<x och x<0
andra ger x-2≤3 => -1≤ x ≤ 5 (här, när jag fick svaret på att x skulle vara mindre eller lika med -1, så resonerade jag mig fram, för att uttrycket skulle få ≤3, hur gör jag algebraiskt? gjorde samma typ av resonemang på den precis ovan med att x<0).
därefter så ritade jag ut dessa gränser på tallinje och ser att x måste ligga mellan -1≤ x < 0 eller 4<x≤5