Absolutbelopp
Hej! Jag förstod inte dagens förklaring av denna bilden under matte genomgången, skulle uppskatta lite hjälp. Vad visar de två linjerna? Jag vet att det har något med att värdet ej kan bli negativt osv.. men vad menas med bilden?
Du kan tänka dig absolutbeloppet som avståndet från noll (origo).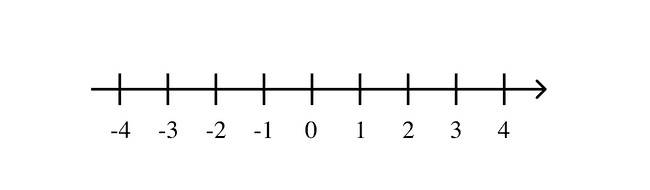
Tänk dig en tallinje. Både -4 och 4 är distans 4 från punkten 0. Det är essentiellt det absolutbeloppet är, hur långt är punkten från 0? Då blir det att alltid är positivt, eftersom en distans alltid är positiv. och är lika långt bort från 0.
Absolutbelopp definieras enligt följande:
- om
- om
Det betyder att kan skrivas då och då
Bilden visar alltså grafen till
Så om vi t.ex. har blir alltså y = 4? Och om jag förstått rätt, så visar bilden alltså ett lika stort avstånd från origo uppe i y-led, oavsett negativt eller positivt värde i x-led?
zenaa06 skrev:Så om vi t.ex. har blir alltså y = 4? Och om jag förstått rätt, så visar bilden alltså ett lika stort avstånd från origo uppe i y-led, oavsett negativt eller positivt värde i x-led?
Ja. Vi kan säga att y-värdet är avståndet från origo. . Detta berättar att punkten ligger 4 enheter bort från 0.
Men som Yngve skrev är definitionen av absolutbeloppet:
om
om
Hur detta fungerar då, om är positivt är , exempelvis och
Men om , alltså det är negativt, så kommer vi få att . Exempelvis om får vi att eftersom minustecknen tar ut varandra. Man kan säga att den ger tillbaka den "positiva varianten" av det negativa talet
Tack för hjälpen!
Du kan se grafen som två olika räta linjer (egentligen två "strålar").
Till vänster om origo är grafen y = -x, till höger om origo är grafen y = x.
==========
För lite mer komplicerade uttryck kan du använda samma metod.
Om vi t.ex. tar så kan vi använda definitionen av absolutbelopp igen:
- då , dvs då
- då , dvs då
De två strålarna blir då då och då .
Grafen till ser alltså ut så här:

Den geometriska tolkningen av är "avståndet mellan talet x och talet 2".
========
Generellt gäller att uttrycket kan tolkas som "avståndet mellan talet x och talet a".
Det funkar även om a är negativt.
T.ex. kan vi skriva om |x+3| som |x-(-3)| och därmed tolka detta som "avståndet mellan talet x och talet -3".
Pröva gärna att rita grafen till y = |x+1| som träning.



