Absolutbelopp

Din ritning är ytterst nära rätt, bara en enkel justering som saknas. Jag skulle säga såhär:

Börja med att rita upp | x-2 | samt | x-1 | på samma koordinatsystem. Efter du ritat upp de två summerar du dem till en graf. För vilka värden på x har grafen konstant y-värde? Vad får grafen för lutning? 

Det är fel på lutningen på vänstra delen av din kurva.

Jag har väldigt svårt för absolutbelopp. Hur ska jag tänka när du säger börja rita upp |x-2|. Hur vet jag hur den ser ut? Behöver jag inte veta vad y är? Har du lust att förklara hur du skulle gjort och tänker? ☺️

Kort och gott kan man säga att "absolutbelopp" gör alla negativa värden till positiva värden, dvs speglar dem på x-axeln.

Betrakta grafen till y = x:

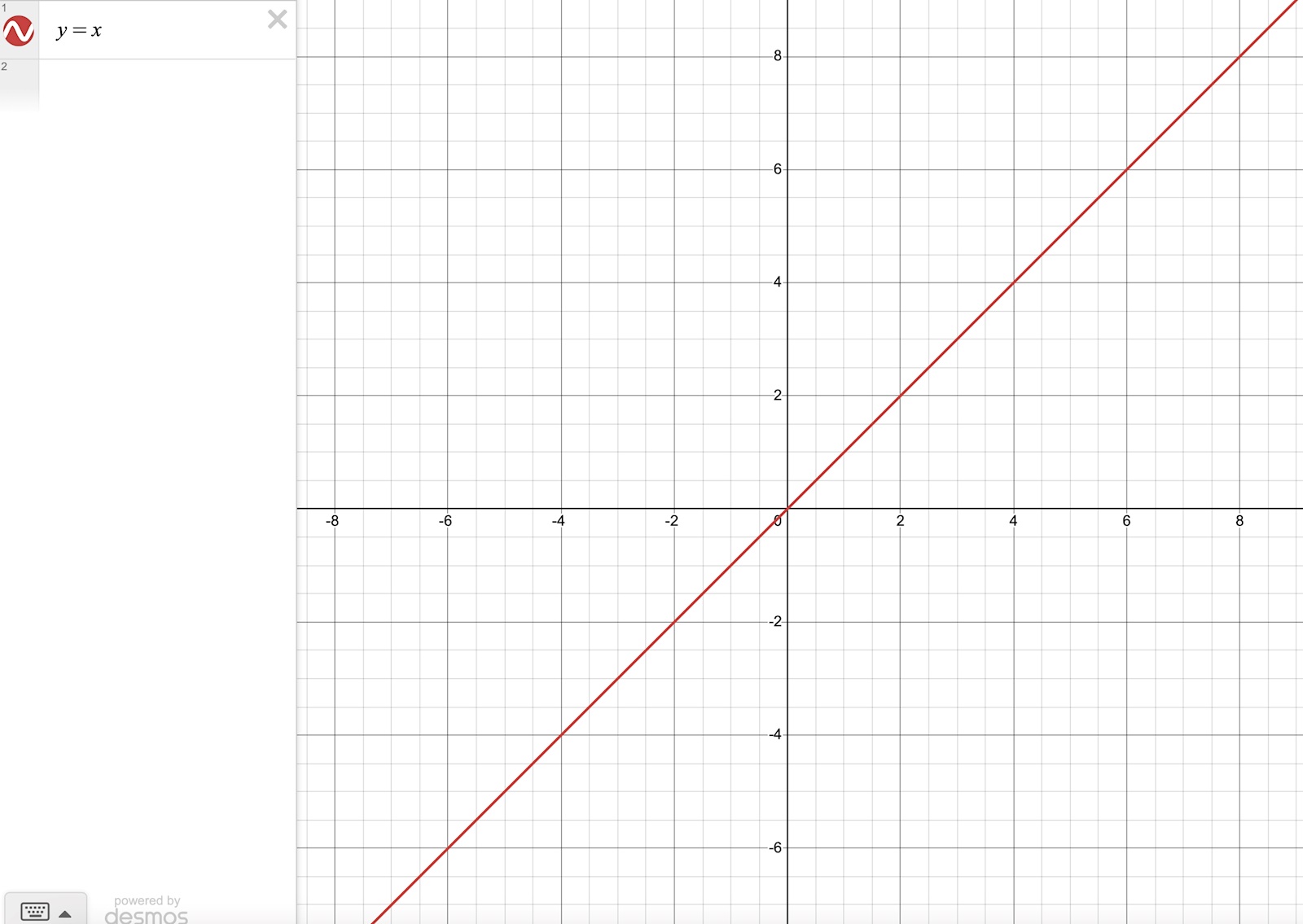
Absolutbeloppet av x ser då istället ut såhär:

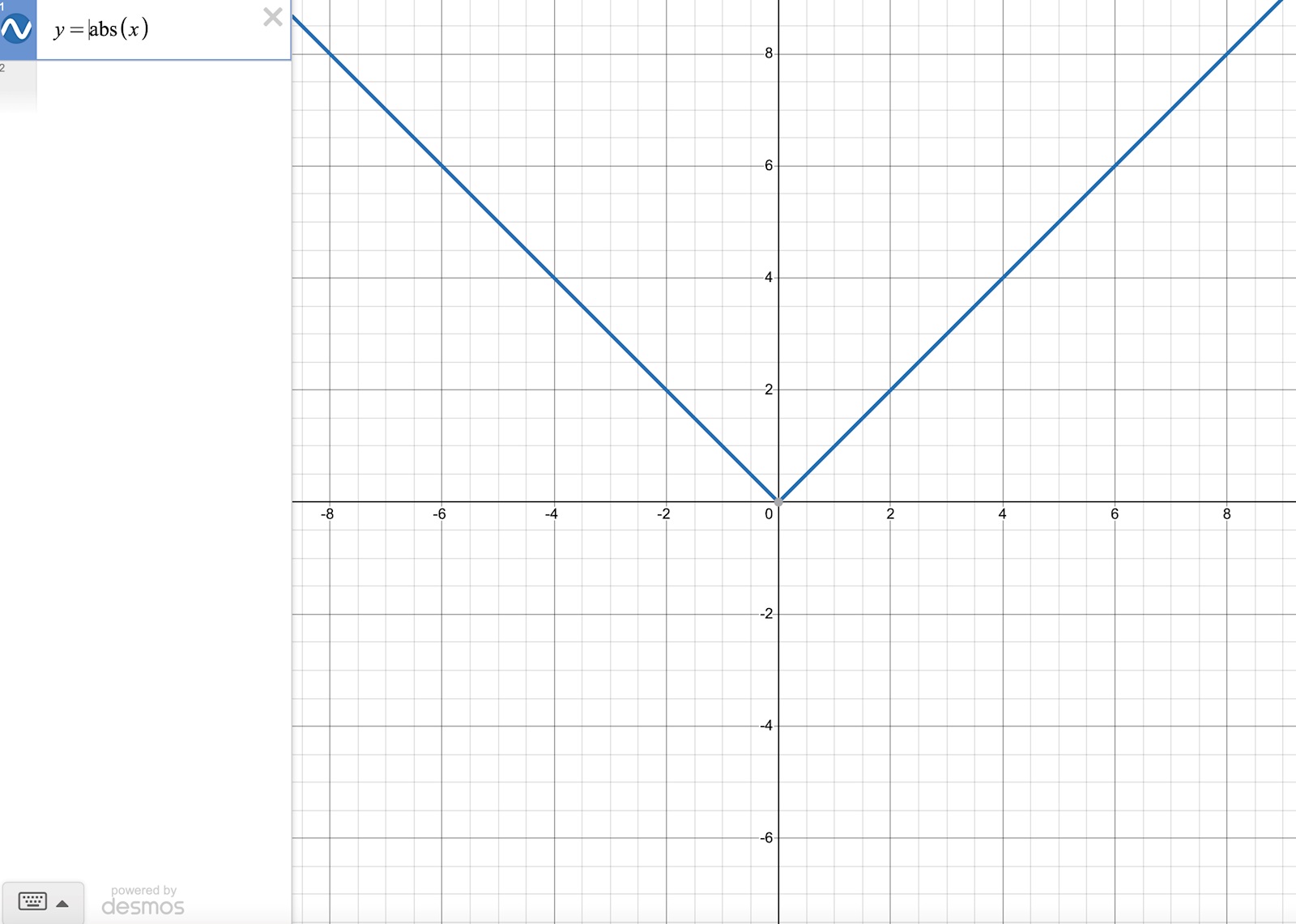
Alltså har de negativa värdena blivit positiva. Hur blir det på formen y = | x-c | då där c är en konstant? Jo, geometrisk sätt kan det tolkas som att y är lika med avståndet från x till c.

Säg att vi har y = | x-2 |. Vad är y då x = 2?

Svar: Avståndet från 2 till 2 är lika med 0. Om x är 5 då? Avståndet från 5 till 2 är 3. Så y = 3 då x = 5.

Alltså har konstanten c "förskjutit" kurvan till y = | x | c åt höger. Betrakta grafen nedan till y = | x-1 |:

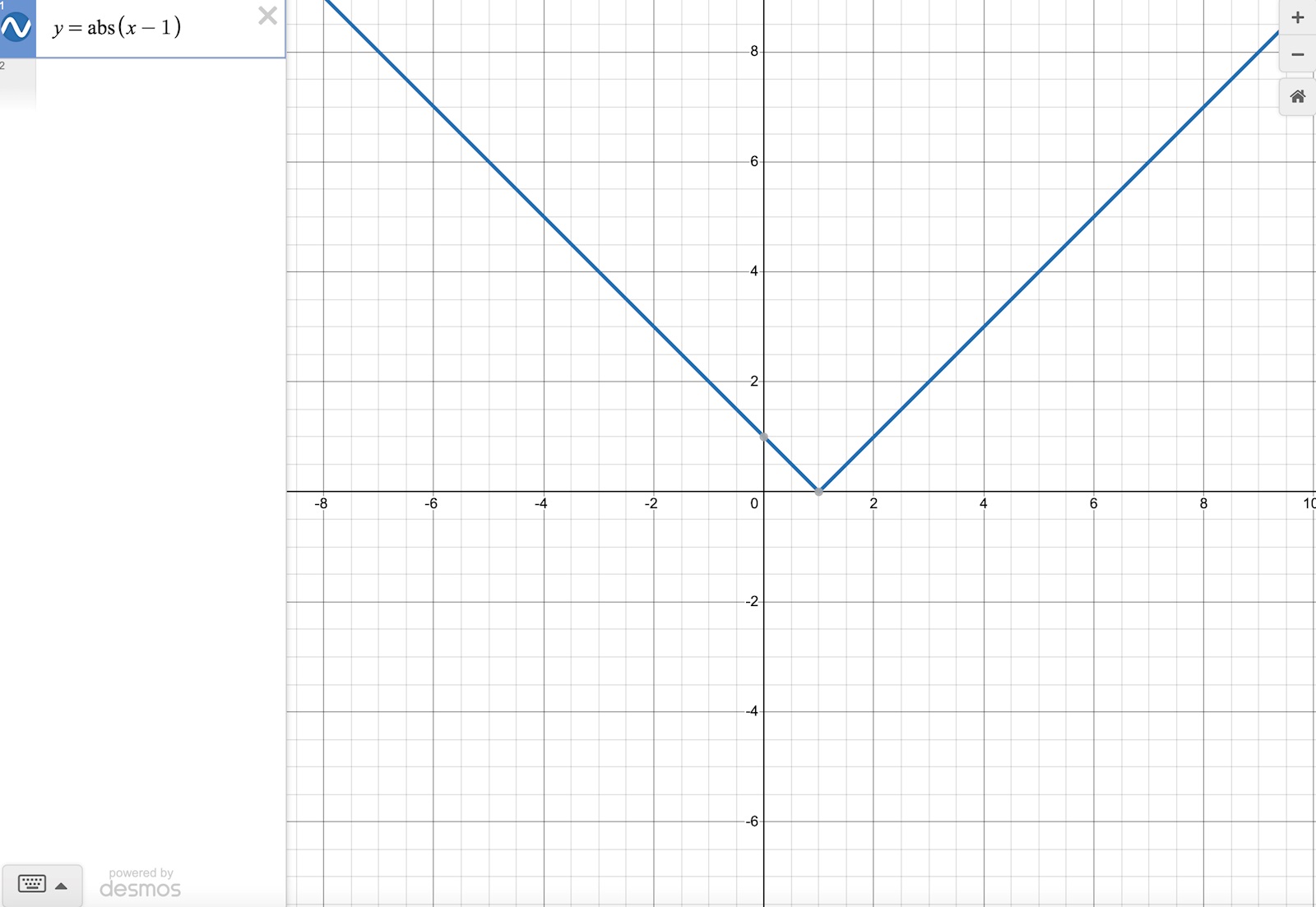
Hur blir det med y = | x + 1 | ? Då sker förflyttning åt vänster istället, eftersom man kan skriva det som y= | x - (-1) |. Värdet på c förskjuter grafen med ett steg c i x-led.

Om man ritar ut graferna till | x - 1 | och y = | x - 2 | blir det såhär:

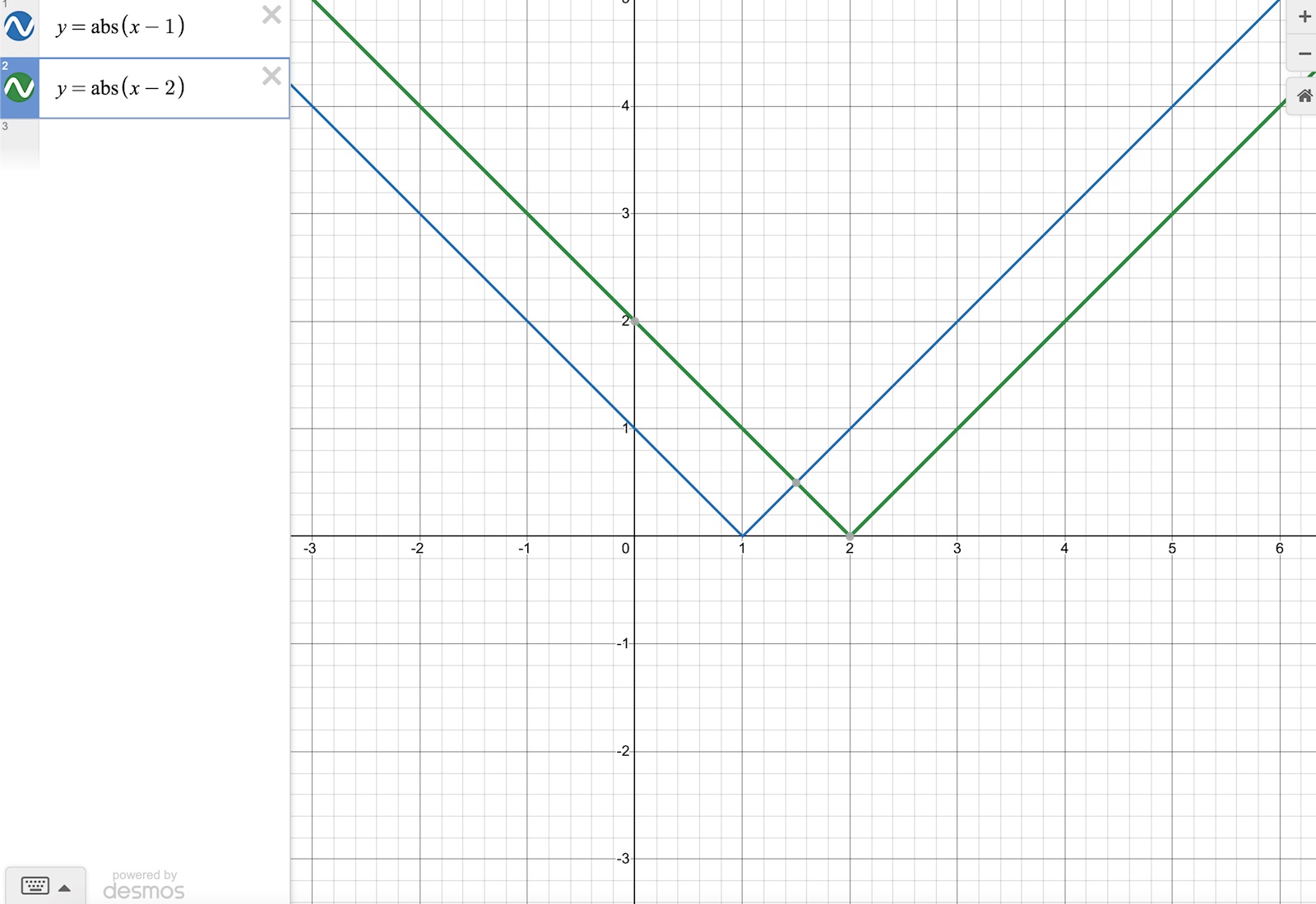
Vad händer då man summerar de? Jo, mellan x = 1 och x =2 blir ju summan alltid 1. Utanför det intervallet så summerar man deras lutning så det ökar dubbelt så snabbt än var för sig. Se grafen nedan:

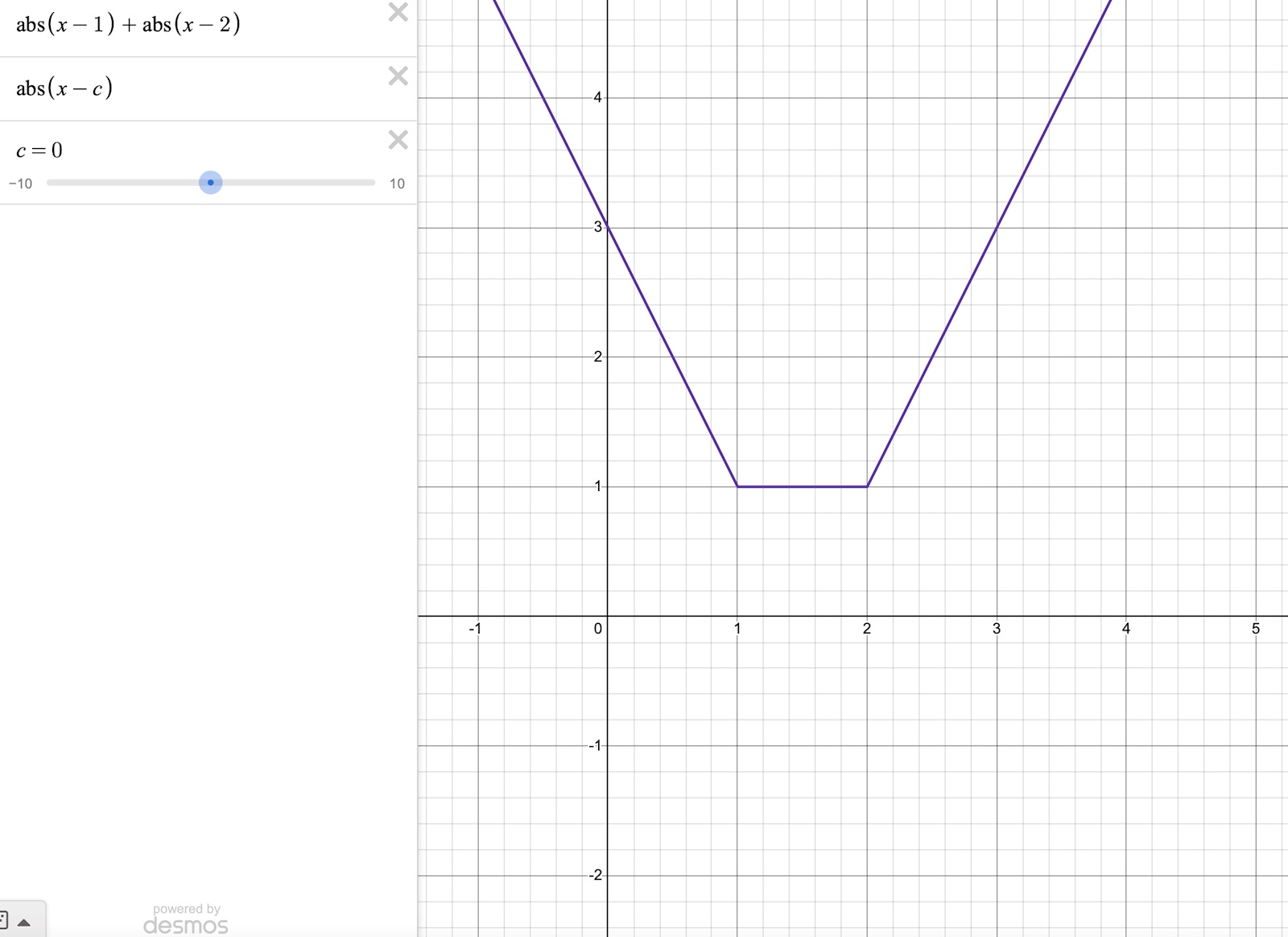
Vill du laborera lite själv med absolutbelopp så är länken till verktyget följande:

https://www.desmos.com/calculator/i3jquyfao3

Hoppas det här var till någon hjälp :)

Johanna93 skrev:

Jag har väldigt svårt för absolutbelopp. Hur ska jag tänka när du säger börja rita upp |x-2|. Hur vet jag hur den ser ut? Behöver jag inte veta vad y är? Har du lust att förklara hur du skulle gjort och tänker? ☺️

Du har redan gjort det stora arbetet, nämligen en algebraisk lösning.

Utnyttja den, eller åtminstone den del där du sätter upp de tre fallen/intervallen.

Om vi sätter $f(x)=|x-2|+|x-1|$ så har du kommit fram till att

• I intervallet $x < 1$ så gäller att $f(x)=-(x-2)-(x-1)=-2x+3$
• I intervallet $1\leq x < 2$ så gäller att $f(x)=-(x-2)+(x-1)=1$
• I intervallet $x\geq2$ så gäller att $f(x)=(x-2)+(x-1)=2x-3$

Nu kan du enkelt rita de tre linjerna som utgör grafen till $y=f(x)$ i respektive intervall.

Tack för era förklaringar! Nu förstår jag lite mer! 😃