Jag skulle rita upp de båda uttrycken (i samma graf). Då ser man antagligen lösningen direkt. Det är ju även vad uppgiften frågar efter.
Kanske blir det lättare om du stuvar om lite och får ett enda uttryck:
Undersök vad som händer för små x.
En grafisk lösning som sictransit tipsar om är nog den snabbaste och enklaste vägen till svaret.
Om du istället vill lösa uppgiften algebraiskt så kan du göra på följande sätt;
- Hitta "brytpunkterna", dvs de x-värden vid vilka uttrycken innanför absolutbelopptecknen byter tecken.
- För x+1 är brytpunkten
- För x-1 är brytpunkten
- Dela nu med hjälp av dessa brytpunkter in x-axeln i tre olika intervall: , och .
- För vart och ett av dessa intervall: Skriv om olikheten utan absolutbelopptecknen, lös olikheten och förkasta alla lösningar som inte ligger I det aktuella intervallet.
- Kvarvarande lösningar utgör olikhetens lösningsmängd.
============
Jag hjälper dig med det första intervallet:
- I intervallet så gäller att och .
- Det betyder att olikheten här kan skrivas
- Denna olikhet kan skrivas , vilket är ett osant påstående.
- Olikheten saknar alltså lösningar i detta intervall.
Gör nu på samma sätt i de övriga två intervallen.
Skulle du kunna lösa den grafiskt det var frågan till uppgiften.
Tomngu skrev:Skulle du kunna lösa den grafiskt det var frågan till uppgiften.
OK, rita då in de båda graferna och i samma koordinatsystem.
Olikheten är uppfylld för alla där den första grafen ligger under den andra grafen.
Visa dina grafer så hjälper vi dig om du kör fast.
=======
Tips om du är osäker på hur geafen ska ritas: Enligt definitionen av absolutbelopp så gäller det att
- då , dvs då
- då , dvs då
Och motsvarande för .
Men förstår inte varför det blir den grafen
Tomngu skrev:
Har du koll på hur absolutbelopp fungerar, att man "hugger bort minustecknet"?
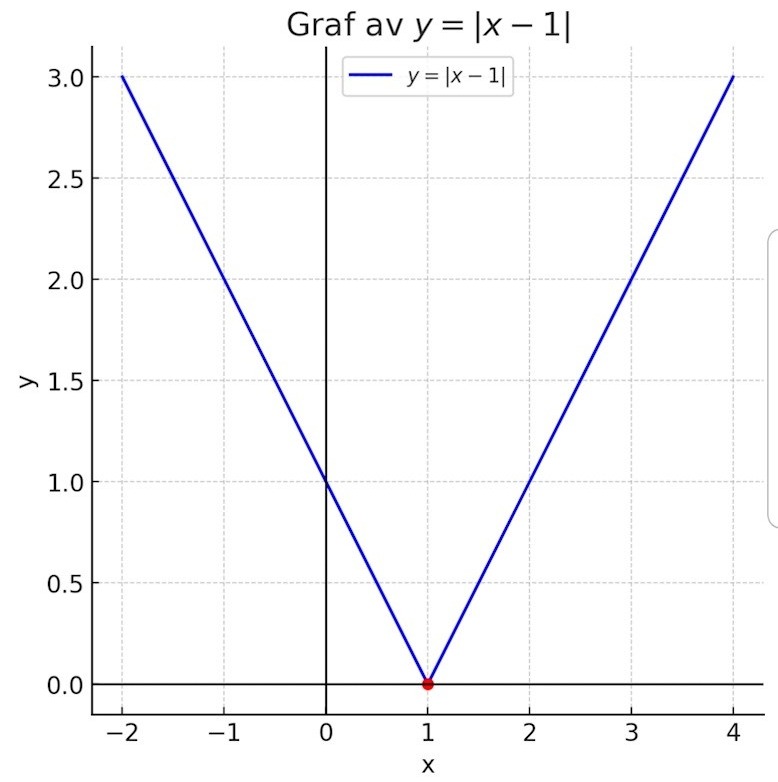
Vi provar för några små x på funktionen y=|x-1|:
x=-1 ger y = |-1-1| = |-2| = 2
x=0 ger y = |0-1| = |-1| = 1
x=1 ger y = |1-1| = |0| = 0
x=2 ger y = |2-1| = |1| = 1
Det ger grafen ovan.
Ok tack.
Hur ska man tolka denna graf detta skär x när y är 1?

Tomngu skrev:Hur ska man tolka denna graf detta skär x när y är 1?
Du har en skärningspunkt, uttrycken har samma värde, i x=0.
Läs sedan vad Yngve skrev i inlägg #5 om hur du skall tolka grafen.
är svaret x≤0 ?
Tomngu skrev:är svaret x≤0 ?
Prova!
Sätt in exempelvis x=-1 i ekvationen och se om det stämmer.
Tomngu skrev:Men förstår inte varför det blir den grafen
Om du är med på det jag skrev i svar #5 då kan du rita grafen till y = 1-x fram till x = 1 och grafen till y = x-1 från och med x = 1.
Du får då grafen i svar #6.
Gör sedan på samma sätt med uttrycket |x+1|.