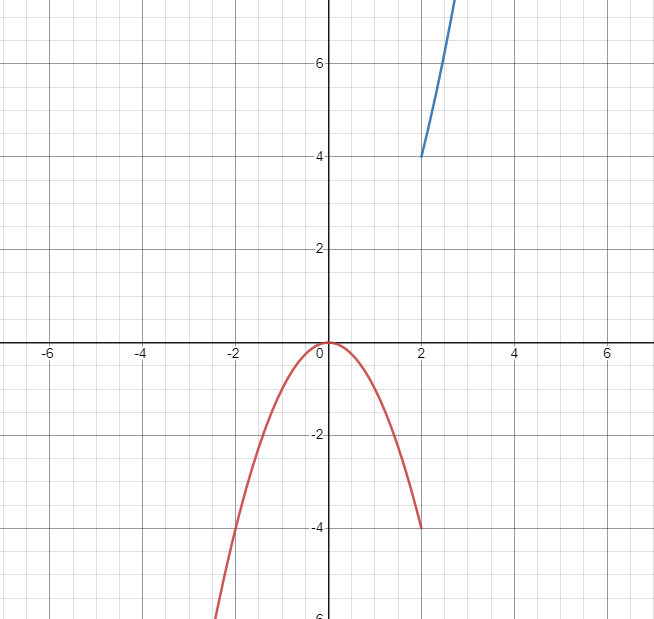
deriverbarhet
Hej skulle behöva hjälp med denna uppgiften hur man räknar?
Vet du vika två villkor som behöver vara uppfyllda för att en funktion skall vara deriverbar i en viss punkt?
Varifrån kommer uppgiften? Är det verkligen Ma3? Jag skulle ha gissat på universitetsnivå.
Smaragdalena skrev:Vet du vika två villkor som behöver vara uppfyllda för att en funktion skall vara deriverbar i en viss punkt?
Varifrån kommer uppgiften? Är det verkligen Ma3? Jag skulle ha gissat på universitetsnivå.
Ja: kontinuerlig, får endast ha en tangent och definierad i punkten.
Ja från matte 3c.
Då kollar du de egenskaperna för var och en av deluppgifterna. Om du behöver mer hjälp, så visa hur långt du har kommit och fråga igen.
Smaragdalena skrev:Då kollar du de egenskaperna för var och en av deluppgifterna. Om du behöver mer hjälp, så visa hur långt du har kommit och fråga igen.
på h(x) är jag lite fast på, för när man ritar upp och kollar på den grafiskt så är den inte alls kontinuerlig? speciellt inte när x = 0
Är h(x) och h'(x) lika från mindre än 2 och större än eller lika med 2?
Grafen måste inte vara kontinuerlig överallt, utan endast runt punkten där du vill derivera. Hur ser h(x) ut runt punkten x=0?
naytte skrev:Grafen måste inte vara kontinuerlig överallt, utan endast runt punkten där du vill derivera. Hur ser h(x) ut runt punkten x=0?
som en glad mun på en en ledsen vid x = 0
Tänker du att grafen ser ut ungefär så här?:
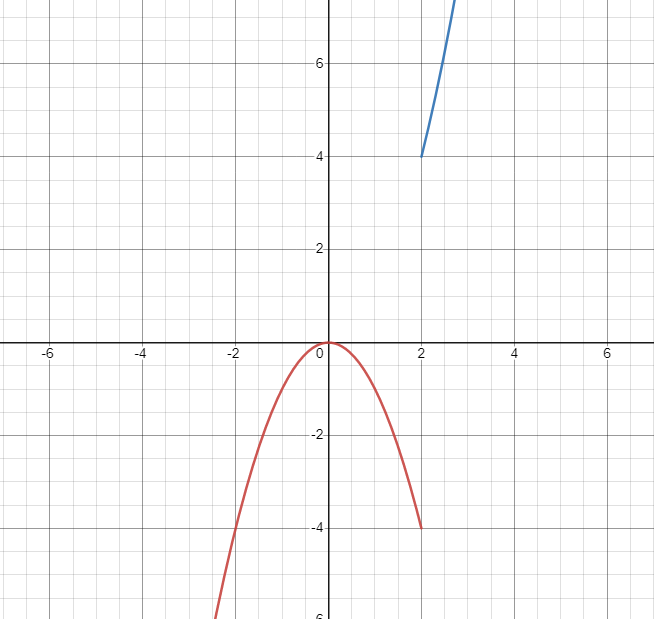
naytte skrev:Tänker du att grafen ser ut ungefär så här?:
ja precis
Bra. Här ser du att grafen ganska uppenbarligen är deriverbar när x=0. Som du ser är den kontinuerlig runt punkten, på både vänster och höger.
naytte skrev:Bra. Här ser du att grafen ganska uppenbarligen är deriverbar när x=0. Som du ser är den kontinuerlig runt punkten, på både vänster och höger.
Jaha, jag trodde en funktion är kontinuerlig när båda "delar" sitter ihop överallt.
Funktionen är inte kontinuerlig, men den är kontinuerlig runt punkten x=0. Det är en skillnad.
Okej nu förstår jag