a) asymptot

y = Ce-2x+ 1/2x
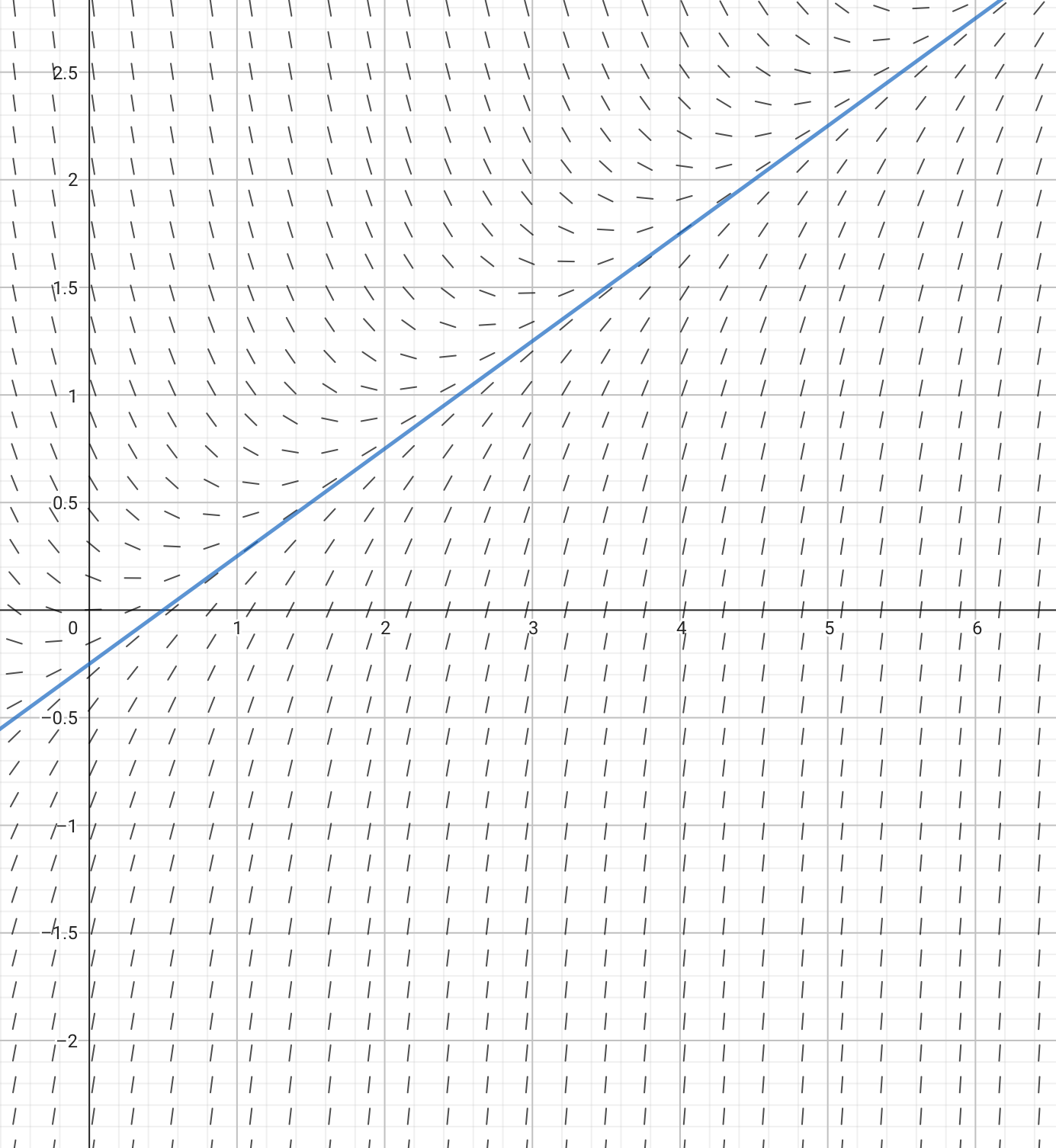
jag har justerat konstanten C och har fått den räta linjen y= 0.5x -0,25. dock var svaret att asympotetens ekvation var y=0.5x-0.25. Jag förstår inte om jag har justerat C och fått y= 0.5x -0,25 innebär det inte då att det är en lösningskurva till diffekvationen?
Det kan inte vara en rät linje om inte C=0. Om e-2x är något annat än noll så är det icke en rät linje!
så om Ce-2x = 0 är det inte en lösningskurva till diff.ekvationen?
fysik3 skrev:så om Ce-2x = 0 är det inte en lösningskurva till diff.ekvationen?
Undrar du alltså om y = Ce-2x -(1/2)x är en lösning till y' = x-2y trots att Ce-2x = 0?
I så fall: Pröva1
Om Ce-2x = 0 så måste C = 0.
Det innebär att y = -(1/2)x.
Är det en lösning till diffekvationen?
den allmänna lösningen är y = Ce-2x+0,5x-0,5 jag tänker att om C=0 får vi en lösningskurva som agerar som en rät linje. lösningskurvan har ekvationen y=0,5x - 0,5 Finns det något krav på att C 0?
Notera att e-2x går mot noll så x mot oändlighet, så du får en asymptot oavsett vilket värde på C som du har.



