A = A och B??
Hej! hur ser man från vändiagrammet att ? Jag förstår Den första att A = A och inte B, men hur kan A = A och B?

Tack på förhand!
I Venn-diagrammet är den första delen den som är markerad med diagonala streck och den andra delen har horisontella streck. Tillsammans utgör de precis A.
Tack för svar! Men den med horisontella streck utgör ju bara en del av B så hur kan de skriva att A = A+B? Borde inte detta påstående innebära hela B?
innebär snittet, dvs det område som finns i båda mängderna.
Varför tycker du att det står A = A+B?
Calle_K skrev:innebär snittet, dvs det område som finns i båda mängderna.
Ah okej tack! då förstår jag:)
Laguna skrev:Varför tycker du att det står A = A+B?
Förlåt jag råkade skriva + men menade snittet!
OK. Varför tycker du att det står A = A snitt B?
Laguna skrev:OK. Varför tycker du att det står A = A snitt B?
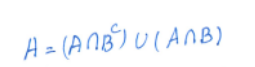
Där står det väll det då A = (A snitt inteB) eller A=(A snitt B)?
Det står "union", inte "eller".
Laguna skrev:Det står "union", inte "eller".
Men innebör inte union att det ska vara det ena eller det andra? dvs A union B innebär A eller B?
Man kan lätt göra fel med "och" och "eller" i både mängdlära, logik och sannolikhetslära.
Ja, "x tillhör (A union B)" är ekvivalent med "(x tillhör A) eller (x tillhör B)".
Så "eller" och "union" har något med varandra att göra, men din tolkning stämmer inte. Jag är inte säker på exakt vad din tolkning är, men om den leder till "A = A snitt B" här så är den fel.
Laguna skrev:Man kan lätt göra fel med "och" och "eller" i både mängdlära, logik och sannolikhetslära.
Ja, "x tillhör (A union B)" är ekvivalent med "(x tillhör A) eller (x tillhör B)".
Så "eller" och "union" har något med varandra att göra, men din tolkning stämmer inte. Jag är inte säker på exakt vad din tolkning är, men om den leder till "A = A snitt B" här så är den fel.
Ah okej:( Vet inte riktigt hur jag ska se unionen då:(
Det är svårt att använda ordet "eller" korrekt i alla sammanhang.
Vardagligt: "A eller B" kan betyda antingen A eller B. (exklusivt, dvs inte båda)
eller inklusivt: A eller B eller båda
Mängden (A union B) innehåller
alla element som tillhör A eller B eller båda
dvs alla element som tillhör någon av mängderna A och B
Säkrast att dela in unionen i disjunkta delar: A + B =. ABc + AB + AcB
Nu använde jag. skrivsättet. A + B för (A union B) och AB för (A snitt B).
Det är lättare att skriva så i vårt forum.
Det ursprungliga uttrycket (#1) kan då skrivas A = ABc + AB
Rita Venn-diagram!
(efter John Venn, se. https://sv.wikipedia.org/wiki/Venndiagram )
Arktos skrev:Det är svårt att använda ordet "eller" korrekt i alla sammanhang.
Vardagligt: "A eller B" kan betyda antingen A eller B. (exklusivt, dvs inte båda)
eller inklusivt: A eller B eller bådaMängden (A union B) innehåller
alla element som tillhör A eller B eller båda
dvs alla element som tillhör någon av mängderna A och BSäkrast att dela in unionen i disjunkta delar: A + B =. ABc + AB + AcB
Nu använde jag. skrivsättet. A + B för (A union B) och AB för (A snitt B).
Det är lättare att skriva så i vårt forum.Det ursprungliga uttrycket (#1) kan då skrivas A = ABc + AB
Rita Venn-diagram!
(efter John Venn, se. https://sv.wikipedia.org/wiki/Venndiagram )
Tack så mycket! nu förstår jag:)
Ett gammalt klassiskt skämt är när matematikern som får frågan från en servitris om hen vill ha kaffe eller te svarar "ja". Matematiskt korrekt, men oanvändbart för servitrisesn.




