5 bokstäver ordnande i en ring
Hej!
Jag behöver hjälp med denna uppgift:
I figuren är de 5 bokstäverna A-E ordnade på samma sätt i en ring med 5 positioner.
En vridning av ringen påverka inte ordningen.
a) På hur många sätt kan man ordna bokstäver i en ring med 5 positioner?
Det jag inte fattar är varför fakulteten delas med 5.
Tack i förhand.
Välkommen till Pluggakuten! Fakulteten delas med fem, eftersom vridningen inte påverkar ordningen. Titta på följande biler:
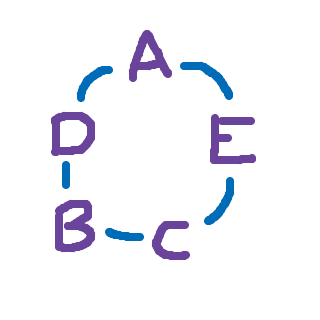
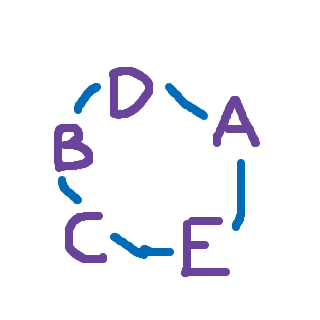
Ordningen är densamma, men bokstäverna har "vridits" ett femtedels varv. Det finns fem olika "varv", som alla är samma ord. Därför divideras fakulteten med fem.
Man kan ju försöka motivera divisionsoperationen från urskrivning. 5!=120 är rätt många att skriva ut men 4!=24 fallet kan man kolla på.
Låt säga att man skrev ut alla permutationer av fyra bokstäver
ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB, DCBA
så skulle flera av dessa motsvara samma "ring". Fundera på hur många som är "dubbletter" och generalisera till fem bokstäver.



