Du har skrivit upp ett bra uttryck: a2/4-a>0. Om detta gäller har ekvationen 2 dubbelrötter.
Detta är i sin tur en andragradsekvation som måste lösas. Ett tips är att rita upp den i en graf så får du se ungefär vilka värden a måste ha.
Calle_K skrev:Du har skrivit upp ett bra uttryck: a2/4-a>0. Om detta gäller har ekvationen 2 dubbelrötter.
Detta är i sin tur en andragradsekvation som måste lösas. Ett tips är att rita upp den i en graf så får du se ungefär vilka värden a måste ha.
Hur löser jag denna andragradsekvation om jag inte har tillgång till en grafräknare?
Du kan sätta a2/4-a=0 och lösa denna. Det kommer finnas två lösningar till denna ekvation. Med tanke på hur funktionen till VL ser ut kommer de lösningar vi vill åt vara de a som är mindre än den minsta lösningen och större än den stora lösningen.
Försök lösa uppgiften själv härifrån och redovisa din lösning här så kan jag hjälpa till om du fastnar.
Calle_K skrev:Du kan sätta a2/4-a=0 och lösa denna. Det kommer finnas två lösningar till denna ekvation. Med tanke på hur funktionen till VL ser ut kommer de lösningar vi vill åt vara de a som är mindre än den minsta lösningen och större än den stora lösningen.
Försök lösa uppgiften själv härifrån och redovisa din lösning här så kan jag hjälpa till om du fastnar.
Nu vet jag för vilka värden a är lika med 0. Men hur vet jag svaret för a?
Ha en fin dag skrev:Calle_K skrev:Du kan sätta a2/4-a=0 och lösa denna. Det kommer finnas två lösningar till denna ekvation. Med tanke på hur funktionen till VL ser ut kommer de lösningar vi vill åt vara de a som är mindre än den minsta lösningen och större än den stora lösningen.
Försök lösa uppgiften själv härifrån och redovisa din lösning här så kan jag hjälpa till om du fastnar.
Förslagsvis genom en teckentabell.
mrpotatohead skrev:Ha en fin dag skrev:Calle_K skrev:Du kan sätta a2/4-a=0 och lösa denna. Det kommer finnas två lösningar till denna ekvation. Med tanke på hur funktionen till VL ser ut kommer de lösningar vi vill åt vara de a som är mindre än den minsta lösningen och större än den stora lösningen.
Försök lösa uppgiften själv härifrån och redovisa din lösning här så kan jag hjälpa till om du fastnar.
Förslagsvis genom en teckentabell.
Vad är en teckentabell?
En tabell där du undersöker vad för värden på a som ger uttrycket olika tecken. Ofta tittar man på intervall. I detta fall vet du att a=0 och a=4 ger uttrycket värdet 0.
Vad får uttrycket för tecken då a<0, 0<a<4 och a>4?
Mrpotatoheads förslag var bra
Men jag tror att det blir lite svårt för en som läser matte 2, eftersom man varken läst om derivata eller om teckentabeller (det kommer i matte 3).
Men har du intresse/tid för att kolla upp det så skadar det ju inte att försöka sig på det! Men själva boken är nog ute efter en annan "enklare" metod.
naturnatur1 skrev:Mrpotatoheads förslag var bra
Men jag tror att det blir lite svårt för en som läser matte 2, eftersom man varken läst om derivata eller om teckentabeller (det kommer i matte 3).
Men har du intresse/tid för att kolla upp det så skadar det ju inte att försöka sig på det! Men själva boken är nog ute efter en annan "enklare" metod.
Ja precis, och vad är det för metod?
Har du koll på hur grafen till funktionen a2-a ser ut? Isfåfall inser du att väldigt stora eller väldigt små (negativa) a gör att funktionsvärdet a2-a blir positivt. Däremellan däremot kan den däremot bli negativ.
naturnatur1 skrev:Mrpotatoheads förslag var bra
Men jag tror att det blir lite svårt för en som läser matte 2, eftersom man varken läst om derivata eller om teckentabeller (det kommer i matte 3).
Men har du intresse/tid för att kolla upp det så skadar det ju inte att försöka sig på det! Men själva boken är nog ute efter en annan "enklare" metod.
Teckentabell har nödvändigtvis ingenting med derivata att göra, som i detta fall. Det är bara ett sätt att både undersöka och redovisa hur teckenbytena ser ut beroende på en variabels värden.
Vill du skippa själva tabellen kan du ju bara fundera över, som jag skrev tidigare, i intervallen:
a<0, 0<a<4 och a>4
Detta är nog den "enklare" metoden du är ute efter.
Calle_K skrev:Har du koll på hur grafen till funktionen a2-a ser ut? Isfåfall inser du att väldigt stora eller väldigt små (negativa) a gör att funktionsvärdet a2-a blir positivt. Däremellan däremot kan den däremot bli negativ.
Det ska vara a2/4 - a.
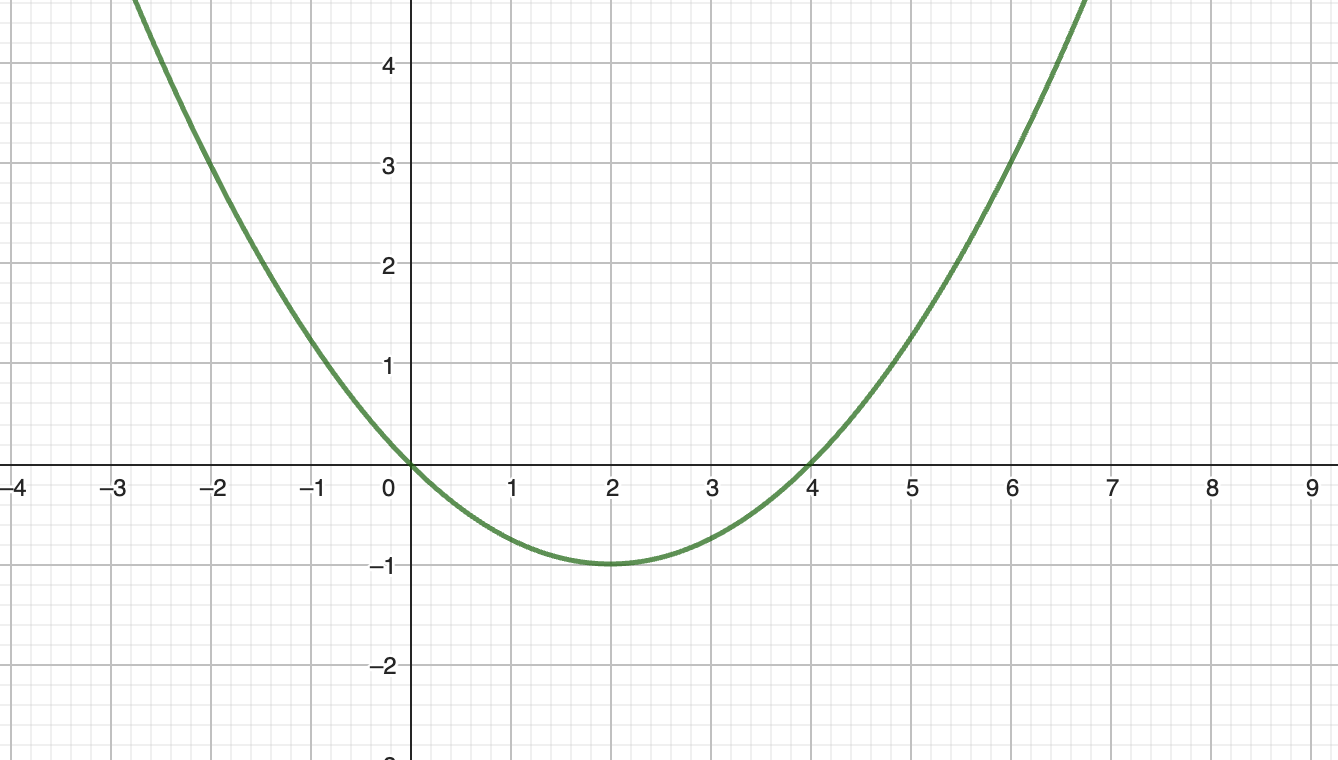
(nu kanske du ser varför du ska undersöka tecknet i de olika intervallen)
nu är jag jätteförvirrad.. vad ska jag göra?
Om f(a) är den gröna funktionen ovan. Vad är dess värde beroende på om a ligger i:
a<0
0<a<4
a>4
Då kan du svara på den ursprungliga olikheten:
"för vilka a gäller a2/4-a>0 och ger ekvationen två reela rötter"?
