36 I tärningsspelet Yatzy kastar man 5 tärningar. (En kåk får man om man har tre tärningar av)
Hej, jag förstår inte hur jag ska riktigt tänka på 36b. Jag har löst uppgiften för det här sättet, men jag förstår fortfarande inte varför man inte ska ha med nCr(5,2) också, för att det finns väl så många sätt att välja resterade två tärningar? Sedan förstår jag inte helt heller varför man inte tar allt gånger två för att man kan väl antingen få de tre först eller de två först (om man ser på dem som grupper, såsom vi gör).
Dessutom skulle jag också vilja veta hur man kan räkna på den här uppgiften med hjälp av gynnsamma över totala fall. Tack!

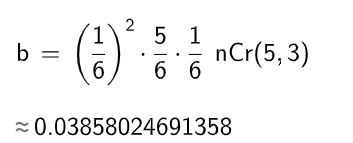
För att svara på din sista fråga: Det finns 30 st olika kåkar man kan få. Vi kan välja värdet 1-6 för tre av tärningarna och för varje sådant val kan värdet på de två resterande tärningarna väljas på 5 sätt.
Dessa kåkar kan uppstå på flera sätt, t.ex. genom att tärningarna visar
4,3,3,4,4
eller
3,4,4,4,3.
Antalet sätt att ordna varje kåk i 5 positioner är 5 choose 3 (vi väljer 3 positioner där tripletten ska in, och då är de två resterande positionerna där vårt par ska in entydigt bestämda). Vi har att 5!/3!2! = 10.
Totalt finns det alltså 30*10=300 sätt att få kåk på.
Det finns totalt 6^5 = 7776 kast.
Vi får att 300/7776 blir ungefär 3.86%.
Tillägg: 17 dec 2024 18:09
Anledningen varför nCr(5,3) eller 5 choose 3 är med i bilden är för att vi har 5 olika tärningar. Även om man i en match Yatzy inte skiljer på tärningarna och knappast följer vilken som är vilken, så är de fortfarande distinkta från varandra. Därför räknar vi t.ex. resultaten 3,3,3,4,4 och 3,4,3,4,3 som två olika utfall. I det första utfallet blev tärning nummer två en trea, men i det andra fallet blev den en fyra.
Tack för motivationen jag är med på hur du tänker. Du förklarade dessutom min första fråga eftersom jag nu förstår att om man har 5 platser att fylla och tre redan är bestämda så finns det bara två platser kvar där det andra numret kan gå, det ger inga nya kombinationer eftersom vi inte bryr oss om ordningen.
Det finns alltså nCr(5,3) olika sätt att välja den första siffran och i alla dessa finns det redan två tomma platser där resterande kommer att gå.
Jag läste fel, du frågade varför nCr(5,2) inte är med också. Låt säga att våra tärningar är tre st 4:or och två 3:or. Om vi tänker att vi har fem positioner att placera in våra tärningar på, så när vi placerat våra tre 4:or på nCr(5,3) sätt, t.ex.
_ 4 _ 4 4,
så måste de två 3:orna in på de två positioner som är kvar. Det kan bara göras på ett sätt. Hade vi haft en trea och en femma kvar att placera, ja då hade vi kunnat göra det på två olika sätt.
Man kan säga det som att positionerna på de tre fyrorna entydigt bestämmer vilket sätt vi får kåken på.
På samma sätt kan vi först välja att placera in treorna. Det kan vi göra på nCr(5,2) = 10 sätt, t.ex.
_ 3 3 _ _
Då är fyrorna positioner bestämda, och vi kan bara placera dem på ett sätt.
Båda sätten ger samma antal: nCr(5,3) = nCr(5,2) = 10.
Ja precis, tack så mycket!



