2253 bestäm tiden

 Hej! Jag har försökt lösa ekvationen vet däremot inte om jag har fått rätt svar, jag förstår inte hur jag ska tolka svaren. Varför har jag fått en negativ tid?
Hej! Jag har försökt lösa ekvationen vet däremot inte om jag har fått rätt svar, jag förstår inte hur jag ska tolka svaren. Varför har jag fått en negativ tid?
Jag har inte kontrollerat dina uträkningar, men jag ser att du har glömt att lägga till periodiciteten.
Med hjälp av den ska du hitta den lösning som ger det minsta positiva värdet på t.
Vad ska periodiciteten vara? Ska det inte vara 2pi?
Nu ser det bättre ut, men varför blev 0,2n till 0,02n?
Och så saknar jag den andra lösningsmängden "pi minus ...".

 Nytt försök
Nytt försök
Nu ser jag att du har skrivit 10pi istället för 100pi.
Och "pi minus ..."-lösningen stämmer inte. Du måste ta "pi minus ..." direkt, inte efter att du har dividerat med 10pi (som ska vara 100pi).
Hur menar du?
Menar du att jag ska ta pi-(10pi(t+1/150)) + 2pi•n
Ja, fast med 100pi istället för 10pi.
Precis som du brukar.
Om det känns rörigt så kan du kalla för .
Ekvationen blir då den betydligt enklare .
Hitta alla lösningar och byt sedan tillbaka till det komplicerade uttrycket.
 Nytt försök
Nytt försök
Ja nu har du med även den andra lösningsmängden på rätt sätt, men du tappar återigen bort periodiciteten och du avrundar lite för mycket i mellanstegen.
Du behöver kolla om n = 1 gör att den sökta lösningen kanske återfinns i t1.
 Nytt försök hur gör jag sen?
Nytt försök hur gör jag sen?
Ser rätt räknat ut men eftersom frågan gäller den lägsta t där funktionen ger 15 så måste du räkna fram t1 med en period för att kontrollera att den inte inträffar före t2.
(Vet inte om du avrundat eller ej när du räknat men se generellt sätt till att du inte avrundar mellanresultat. Antingen räknar du allt på en gång eller så använder du minnet på räknaren.)
Hur ska jag beräkna perioden? Vad är perioden? 2pi?
Det är precis som i de tidigare talen med perioder.
Du har angett korrekt att v1=0,848 + 2pi*n. Du delar sen vinkeln med 100pi, om du gör detsamma med 2pi får du med perioden. Du ska "ta med dig" 2pi*n när du förenklar vidare.
Jaha 2pi/(100pi) ger mig perioden alltså är perioden 0.02
 Det här är vad jag har kommit fram till. Hur ska jag tolka svaret
Det här är vad jag har kommit fram till. Hur ska jag tolka svaret
Kommentarer:
- Eftersom du tar fram närmevärden så ska alla likhetstecken efter arcsin bytas mot .
- "Pi minus"-vinkeln blir ungefär 2,294, inte 2,292.
- När du tog fram den minsta positiva tiden ur t1 så valde du n = 1, eller hur? Då behöver du inte ange periodiciteten längre.
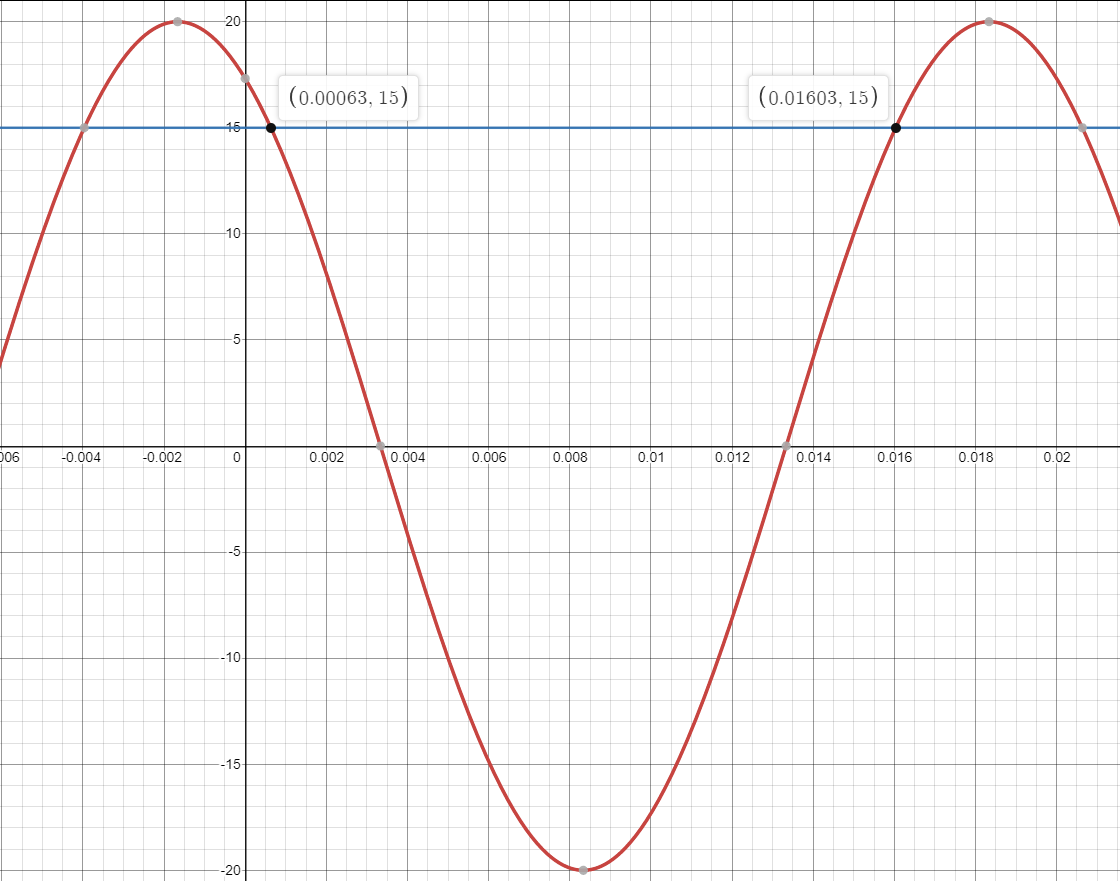
- Den minsta positiva tiden ur t2 bör bli ungefär 0,00063 s, inte 0,063 s. Inte heller här behöver du fortsätta att ange periodiciteten.
Eftersom t2 < t1 så börbtolkningen vara att svaret är ungefär 0,63 ms.

Jag hänger inte med på dina steg
När du tog fram den minsta positiva tiden ur t1 så valde du n = 1, eller hur? Då behöver du inte ange periodiciteten längre.
Den minsta positiva tiden ur t2 bör bli ungefär 0,00063 s, inte 0,063 s. Inte heller här behöver du fortsätta att ange periodiciteten.
Eftersom t2 < t1 så börbtolkningen vara att svaret är ungefär 0,63 ms.
Som jag skrev ovan så handlar uppgiften om att ta fram det minsta t då u=15. Svaret ska alltså vara en (1) tid.
Du använder periodiciteten för att göra den negativa t1 positiv. Då kan den jämföras med t2 och du vet vilken som är minst. Då har du svaret. Det minsta av dina t.
I din förra uträkning hade du t2=0,00063, i den senaste blev det felaktigt 0,063, slarvfel.
Återigen, avrunda inte deluträkningar. Räkna allt i ett svep eller använd minnet på miniräknaren. Avrundningsfelen växer med varje avrundat räknesteg.
Tips: Jag tror du spar tid om du sänker tempot lite. Ett slarvel gör resten av lösningen bortkastad.
Du har redan fått svar av Programmeraren, men jag fyller på med lite steg-för-steg för ökad förståelse:
Uppgiften gäller att hitta det lägsta positiva värdet på tiden som är sådant att den givna ekvationen är uppfylld. Ekvationslösningen ger dig två lösningsmängder, och
- Vi börjar med första lösningsmängden, dvs
- Vi subtraherar från båda sidor och får då lösningsmängden
- För varje möjligt värde på n så får vi en specifik lösning ur (den oändliga) lösningsmängden .
- Vi vill nu ta fram den minsta positiva lösningen ur denna mängd eftersom det kan vara en kandidat till svaret.
- Om vi väljer n = 0 eller negativt värde på n så kommer lösningarna att vara negativa. Det värde på n som ger den minsta positiva lösningen är n = 1.
- Det ger oss lösningen
- Detta kan vara svaret på uppgiften,men innan vi svarar måste vi kolla om kan ge oss en ännu mindre positiv lösning.
Är du med så långt?
 Om n=1 så får jag i t1=0.0161
Om n=1 så får jag i t1=0.0161
om n=1 så får jag i t2=0.0206
Vi söker efter minsta möjliga positiva tid. Alltså är t1 =
~0.016s rätta svaret
men varför fås den minst positiva lösningen om n=1?
"t är tiden i sekunder efter det att strömmen slagits på"
"Efter hur lång tid blir späningen 15V".
Lägsta t efter t=0.
Den minsta positiva lösningen ur t2 är inte 0,0206.
Vad får du ur t2 om n = 0?
Minsta positiva lösningen fås då n=0. Alltså då t2=6.3*10^-4 (sekunder)
Rätt.
Perioden behövdes alltså för att kontrollera inte t1 plus en period inträffade innan t2. Kontrollen var nödvändig eftersom t1<0.
Vi eftersöker den minsta t som är möjlig
Katarina149 skrev:Minsta positiva lösningen fås då n=0. Alltså då t2=6.3*10^-4 (sekunder)
Inte lika med. Ungefär lika med.
Så du ska alltså jämföra den minsta positiva lösningen ur t1 med den minsta positiva lösningen ur t2.
Och sedan välja den minsta av dessa två lösningar.
Så här ser det ut.
- Lösningarna ur t1 är de t-värden där sinuskurvan korsar den horisontella linjen u = 20 i uppförsbacke.
- Lösningarna ur t2 är de t-värdet för vilka sinuskurvan korsar den horisontella linjen u = 20 i nerförsbacke.
- De minsta positiva lösningarna ur t1 och t2 är markerade med ungefärliga koordinater i bilden.