1249 cos
Hej! Hur beräknar man följande oxh får de två vinklarna?
cos2x=cosx
Subtrahera cos(x) från båda sidor. Sedan kan du använda cosinus för dubbla vinkeln för att utveckla cos(2x). Kommer du vidare då?
fner skrev:Subtrahera cos(x) från båda sidor. Sedan kan du använda cosinus för dubbla vinkeln för att utveckla cos(2x). Kommer du vidare då?
Det här e kapitlet innan det. Här vill de att man ska dividera med cos x. Och saken e den att jag fått fram rätt svar, men jag tänker att det borde finnas en lösning till?

är det
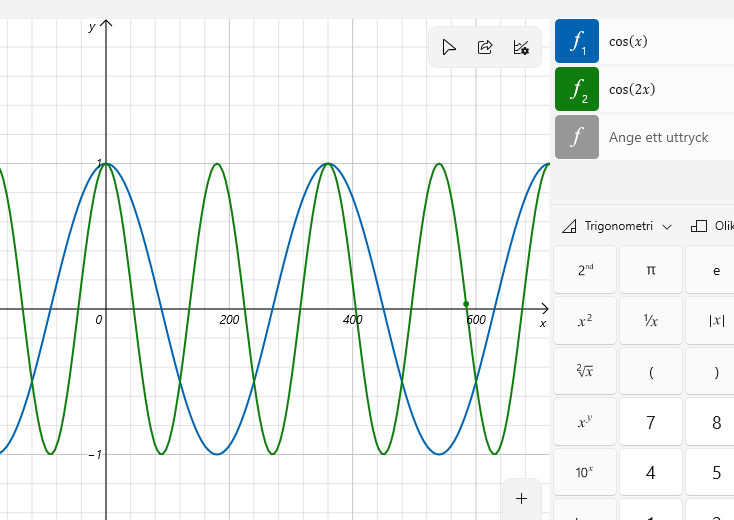
cos2(x) = cos(x)
eller är det
cos(2x) = cos(x) ?
Om det är det andra fallet, tänk på att
cos(a) = cos(-a) vilket ger oss 2 lösningsmängder
Lösningsmängd 1 får vi ur
2x=x+n*360 => x = n*360
Lösningsmängd 2 får vi från
2x = -x+n*360 =>
3x = n*360 =>
x = n*120
Slutligen ser vi att den andra lösningsmängden innehåller även den första
Ture skrev:är det
cos2(x) = cos(x)
eller är det
cos(2x) = cos(x) ?
Om det är det andra fallet, tänk på att
cos(a) = cos(-a) vilket ger oss 2 lösningsmängderLösningsmängd 1 får vi ur
2x=x+n*360 => x = n*360
Lösningsmängd 2 får vi från
2x = -x+n*360 =>
3x = n*360 =>
x = n*120Slutligen ser vi att den andra lösningsmängden innehåller även den första
På vilket sätt innehåller den andra lösningsmetoden även den första?
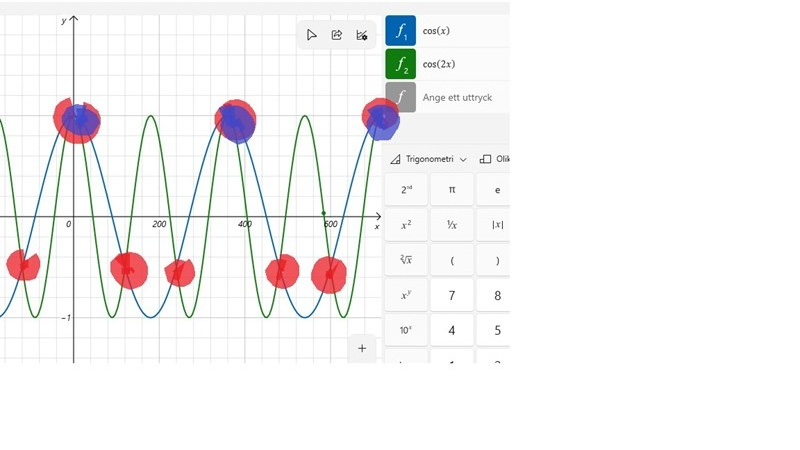
Andra lösningsmängden är rödmarkerad, första är blå. Normalt sett skulle jag rita in dem i enhetscirkeln, men här fanns det redan en så bra bild...

Smaragdalena skrev:Andra lösningsmängden är rödmarkerad, första är blå. Normalt sett skulle jag rita in dem i enhetscirkeln, men här fanns det redan en så bra bild...
Jahaa jag fattar! Men nu k d samma tankesätt, varför lyckas jag inte hitta det andra x för drabba ekvation

Gör en ny tråd om den nya frågan, och lägg in dina uträkningar på rtt håll, tack!
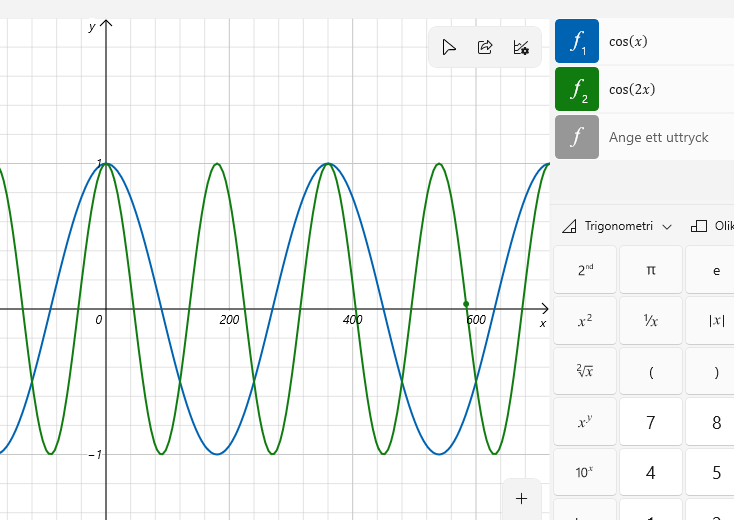
Precis. Gör som Smaragdalena säger! Jag roterar din bild här bara för jag känner mig tvingad nu:).
Ha en fin dag skrev:
[...]
Här vill de att man ska dividera med cos x.
[...]
Det är viktigt att påpeka att det du gör är inte att dividera med cos(x).
I så fall skulle ekvationen ha blivit cos(2x)/cos(x) = 1.
========
Däremot gäller det som Ture skrev i svar #4, nämligen att om cos(a) = cos(b) så gäller det antingen att a = b+n*360° eller att a = -b+n*360°.
Uträkningen bör alltså istället vara så här:
cos(2x) = cos(x)
Detta ger de två lösningsmängderna
2x1 = x1+n*360°, dvs x1 = n*360°
2x2 = -x2+n*360°, dvs x2 = n*120°
Vi ser att lösningsmängd 2 innehåller alla x-värden i lösningsmängd 1, vilket gör att vi kannskriva lösningen som
x = n*120°
Försök att använda ett liknande resonemang i din andra uppgift.
Du skrev i inlägg #3 att man ska dividera bägge led med cos(x) vilket får mig att misstänka att ekvationen kan vara, (som jag skrev i inlägg #4,)
cos2(x) = cos(x)
[ Om man dividerar med cos(x) direkt tappar vi bort en lösningsmängd, (när cos(x) = 0) eftersom vi dividerar med ngt som kan vara 0 ]
Vi kan först konstatera att en lösningsmängd är x = +-90 + n*360, vilket kan skrivas, x = 90 + n*180
sen kan vi dividera med cos(x) och får då den andra lösningsmängden.
cos(x) = 1 med lösningen x = 0 +n*360
Alternativt kan man i den ursprungliga ekvationen istället subtrahera cos(x) i bägge led
cos2(x) -cos(x) = 0 ochg sen bryta ut cos(x) och få
cos(x)(cos(x)-1) = 0 och använda nollproduktmetoden för att få samma lösningar som ovan.
Ture skrev:Du skrev i inlägg #3 att man ska dividera bägge led med cos(x) vilket får mig att misstänka att ekvationen kan vara, (som jag skrev i inlägg #4,)
När jag läste det så misstänkte jag att Ha en fin dag trodde att man kunde "stryka cos" (och bara få kvar 2x = x), vilket man ju inte kan.