1245 Visa att för alla heltal
Hej, jag förstår allt fram till tredje raden efter induktionsantagandet. Jag förstår inte varför de har tre termer efter ..., det ska val bara vara 1/(2p) och 1/(2p+1)? Varför har de med termen 1/(2p+2)? Jag förstår att att den första termen blir till den andra termen, alltså 1/(p+1) blir till 1/(p+2), eftersom man sätter n=p+1, men jag förstår inte hur detta skulle förklara varför man har med tre termer efter "...".
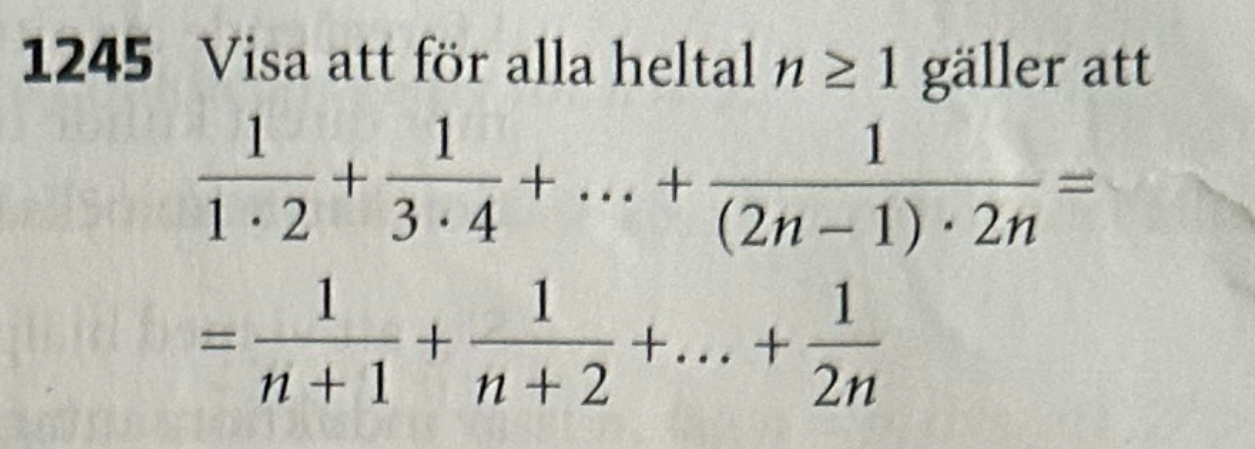
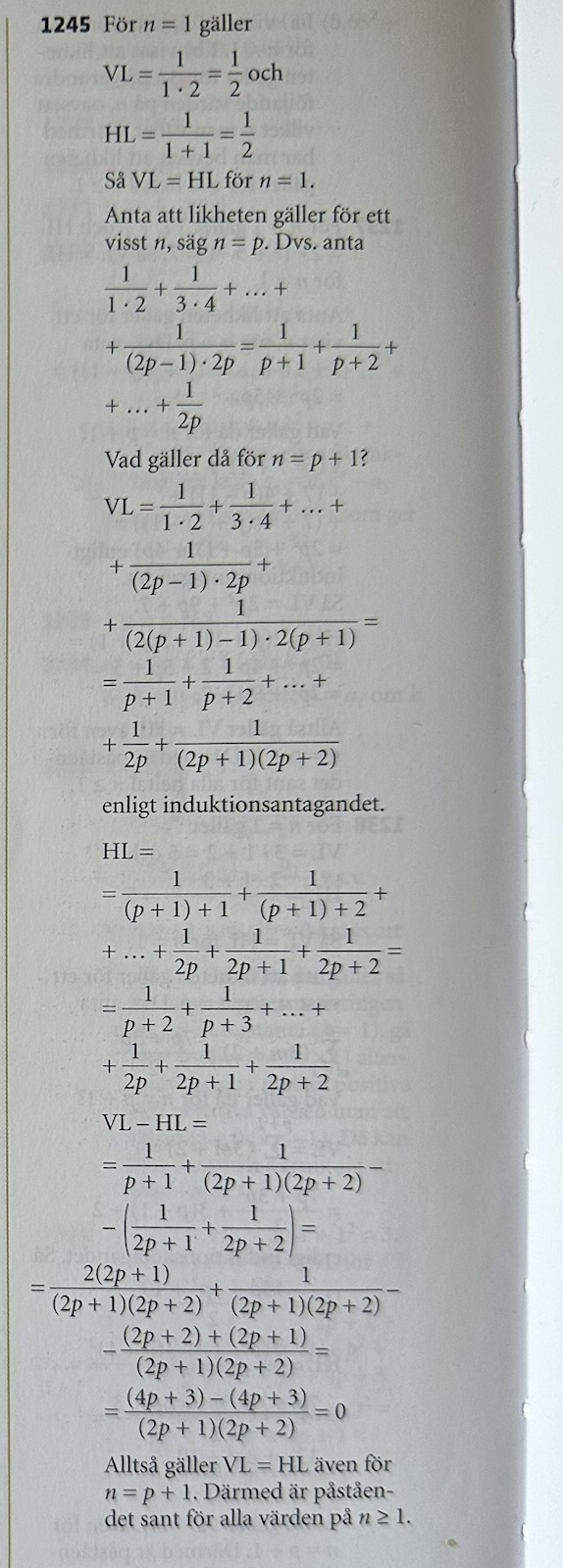
Man kan se det som att i likheten man ska visa och specifikt i HL så ska man ha med alla bråk 1/(n+1) ända tills 1/2n ska vara med. Säg att man hade undersökt fallet då vi har n=4. HL ger då 1/5+1/6+1/7+1/8, dvs bråken med alla från 5 till och med 8 i nämnaren. Säg att vi nu hade ökat n med 1 så vi får n=4+1=5. Vi kommer då få 1/5+1/6+1/7+1/8+1/9+1/10, där vi ser att då har två nya termer 1/9 och 1/10 tillkommit. Så för att svara på frågan så för heltal 1 vi lägger till n så kommer vi få två extra termer (som i min liknelse är 1/9 och 1/10). Dessa Vill vi ta med i induktionsbeviset för att visa på vad som är nytt men vi vill också ta med den senaste termen (som i min liknelse motsvarar 1/8). Av den anledningen så kommer det vara fördelaktigt att ta med 3 termer i beviset och det är därför som (antar jag) facit har gjort så. Hoppas att det reder ut några frågetecken angående facit-framställningen.
Vänta så menar du att det är nödvändigt att ha med tre p-termer eller inte?
Jag hade nog haft med tre stycken termer för att det sammanfaller naturligt med att man kombinerar antagandet (där vi endast behåller en term) med påståendet (där två till termer tillkommer). Man behöver dock inte ha med dessa termer utan man hade absolut kunnat ha endast den sista av de tre men det förutsätter att man förstår vad som har hänt från steget innan. Sammanfattningsvis, nej man behöver inte men för tydlighetens och förståelsens skull så hade jag haft med det.
Fast skulle inte det ändra likheten om man hade/inte hade med en term i VL?
Vet inte om jag förstår rätt men jag tänker att om man har ett uttryck så betyder detta samma sak som
. Det handlar egentligen om att när man har tre prickar att mönstret ska vara uppenbart och vad som eventuellt har ändrats.
Jaha jag förstår din poäng, ska förklara göra uppgiften igen och se om jag förstår. Skriver här sen.
Jag löste uppgiften nu och är med på hur det fungerar. Jag vet inte riktigt varför facit har delat upp 1/((2p+1)(2p+2)) i två olika termer men det gjorde inte jag i alla fall. Men när jag väl hade skrivit om VL med hjälp av HL från induktionsantagandet kunde jag ta VL-HL och visa att det blir lika med noll. Därför måste VL=HL i induktionssteget.
Tack för hjälpen, fick också hjälp från min mattelärare i skolan.


