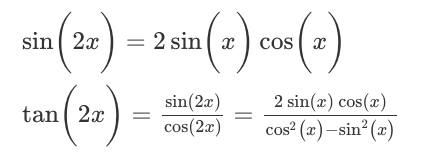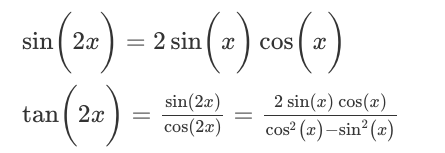(1-2 tan x/ sin 2 x ) ² = ( 1- 2 tan x/ tan 2 x ) ²?
Hur börjar man lösa denna uppgiften. Jag har fastnat på den jättelänge.
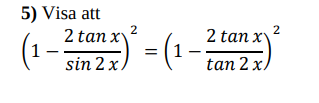
Jag har en viktigt fråga. Varför använder man sin, cos och tan i en lösning? Tycker bara att de står där bara så. Eller har de en betydelse?
Och när det står likhetstecken mellan två lösningar ska man börja med en och sedan den andra eller gör man båda samtidigt i en och samma lösning?
Vet att man kan använda.
Variabelsubstitutionen:
Sedan utnyttja det med följande identitet,
Ibland är det enklast att börja med VL och modifiera det tills man kommer fram till HL. Ibland är det enklast att börja med HL och modifiera det tills man kommer fram till VL. Ibland är det enklast att börja med båd VL och HL, och modifiera dem tills man kommer fram till samma sak på mitten.
För det mesta är det en bra idé att börja med det som ser krångligast ut och försöka göra om det till det enklare uttrycket.
I ditt fall skulle jag nog börja från båda hållen och göra om allting till bara sin(x)-termer, om det går.
Jag måste förstå något som jag aldrig har förstått. Hur och varför omvandlar man från sin till cos t.ex eller från tan till sin. Den viktigaste fråga är HUR?
Varför: För att bara ha EN krånglig variant att syssla med.
Hur: tan(x) = sin(x)/cos(x), trig.ettan, formler för dubbla vinklar, additionsformler (och kanske någon mer som jag inte kommer på just nu)
Är detta rätt?
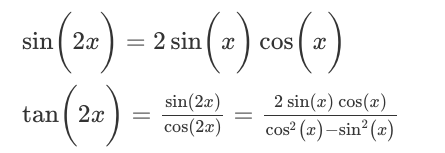
När jag förenklade fick jag att båda sidorna blev,
Om
så är antingen
eller
Här är bara det senare alternativet möjligt.
Dr. G skrev:Om
så är antingen
eller
Här är bara det senare alternativet möjligt.
Förlåt men förstod inte. Vad ska jag göra med den informationen du gav mig?
Du kan ta bort kvadraterna och byta tecken på ett led, men du kanske löste det på annat sätt.
Dr. G skrev:Du kan ta bort kvadraterna och byta tecken på ett led, men du kanske löste det på annat sätt.
Jag förstod att, detta är en kvadrant.
Hur ska jag bryta ut det?
Med kvadraterna menar Dr. G det upphöja, som i a2 och b2 , du får bort dessa genom att ta roten ur.
Kvadrant är en annan sak, det är det du skrev om i inlägg #10.
naturnatur1 skrev:Med kvadraterna menar Dr. G det upphöja, som i a2 och b2 , du får bort dessa genom att ta roten ur.
Kvadrant är en annan sak, det är det du skrev om i inlägg #10.
Ahaa. Är jag färdig med uppgiften eller är det bara det jag gjorde?
ii_noor06 skrev:Är detta rätt?
När jag förenklade fick jag att båda sidorna blev,
.?
ii_noor06 skrev:ii_noor06 skrev:Är detta rätt?
När jag förenklade fick jag att båda sidorna blev,
.?
Ja, du kan skriva om VL som
och HL som
vilket visar att likheten stämmer.
Aha tack!
Hej hur lyckades ni skriva om HL till (1/cos^2x-1)^2? Jag har fastnat på den här frågan med
pizzapi skrev:Hej hur lyckades ni skriva om HL till (1/cos^2x-1)^2? Jag har fastnat på den här frågan med
Gör en egen tråd och visa hur långt du har kommit. Tips: använd formeln "sinus för dubbla vinkeln".