1.102 omskrivning av trigonometrisk formel, Asin2xcosv+Acos2xsinv till 3cos2x-4sin2x
 Jag har kört fast på uppgiften gör använder sinus för dubblavinkeln baklänges.
Jag har kört fast på uppgiften gör använder sinus för dubblavinkeln baklänges.

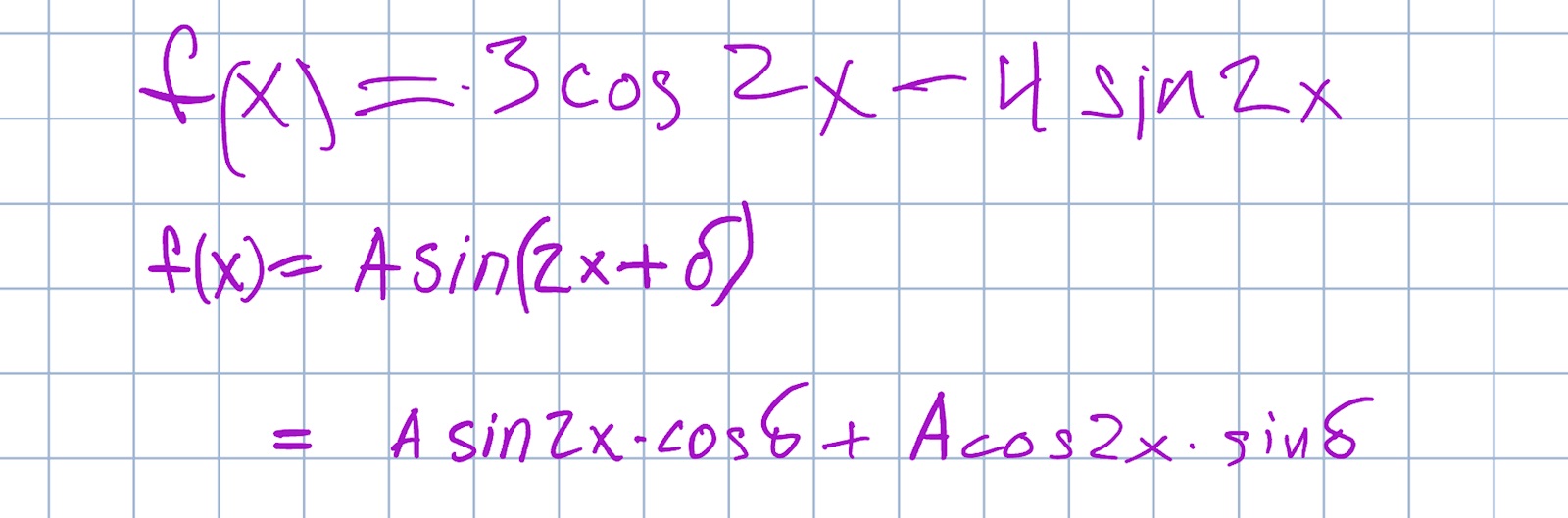
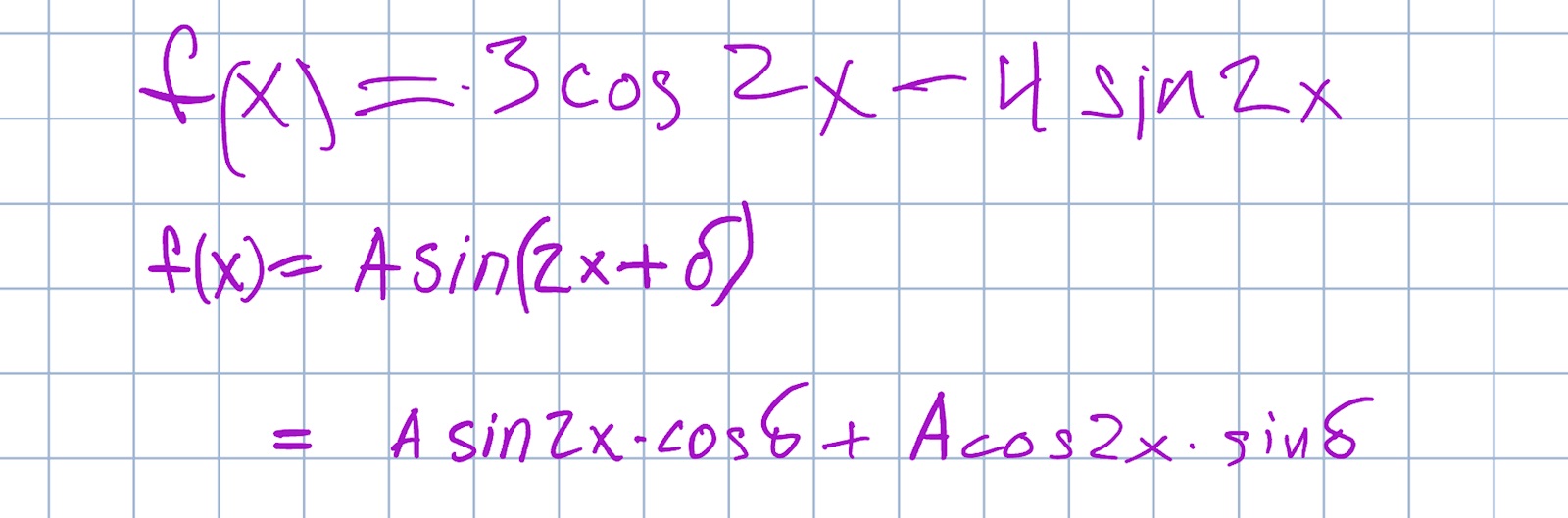 Jag förstår inte hur jag ska från Asin2xcosv+Acos2xsinv till 3cos2x-4sin2x
Jag förstår inte hur jag ska från Asin2xcosv+Acos2xsinv till 3cos2x-4sin2x
Hjälp uppskattas. :D
vänligen,
Philip
Du har alltså kommit fram till att samt att . Det kan vi sammanfatta i en hjälptriangel så här:

Vad händer om du t.ex. skapar en trigonometrisk etta genom att addera kateterna i kvadrat? Vad blir alltså värdet på ?
Kan du sedan identifiera värden på och ?
PS; Jag tror att du egentligen ska använda den från gymnasiet kända formeln
, där och osv, men ditt lösningssätt går också bra!
D4NIEL skrev:Du har alltså kommit fram till att samt att . Det kan vi sammanfatta i en hjälptriangel så här:
Vad händer om du t.ex. skapar en trigonometrisk etta genom att addera kateterna i kvadrat? Vad blir alltså värdet på ?
Kan du sedan identifiera värden på och ?
PS; Jag tror att du egentligen ska använda den från gymnasiet kända formeln
, där och osv, men ditt lösningssätt går också bra!
Tillägg: 8 sep 2023 22:06
Till att börja med förstår jag inte hur du kommer fram till hjälptriangeln sidorna/värdena till hjälp triangeln, hur får du fram dem?
Det är bara att parvis jämföra termerna som innehåller för sig och för sig.
Du har
Detta ska på något vis bli
Om du nu fokuserar på -termen och tänker dig att den ska ha samma koefficient i båda uttrycken ger den ekvationen:
Vad ska anta för värde för att det ska passa ihop?
D4NIEL skrev:Det är bara att parvis jämföra termerna som innehåller för sig och för sig.
Du har
Detta ska på något vis bli
Om du nu fokuserar på -termen och tänker dig att den ska ha samma koefficient i båda uttrycken ger den ekvationen:
Vad ska anta för värde för att det ska passa ihop?
Tack! Jag förstår nu har du får fram ekvationerna till kateterna. Hur går jag vidare för att bilda en enhetscirkel. Tänker att jag på våg sätt måste få katetern till 1.
Tillägg: 8 sep 2023 22:37
Jag får att A=1/5 de ges en enhetscirkel och där med ser uppgiften ut att vara löst. tack!
Njaeä, Amplituden blir inte

